题目内容
17.已知抛物线y2=4x,A、B分别是抛物线上位于x轴上、下两侧的点,且A、B在抛物线准线上的射影点分别为C、D.$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{9}{4}$(其中O为坐标原点),则$\overrightarrow{OC}$•$\overrightarrow{OD}$=-17.分析 求得抛物线的焦点和准线方程,设A($\frac{{m}^{2}}{4}$,m),B($\frac{{n}^{2}}{4}$,n),(m>0,n<0),运用向量的数量积的坐标表示,可得mn=-18,求得C,D的坐标,运用向量数量积的坐标表示即可得到所求值.
解答 解:抛物线y2=4x的焦点为(1,0),准线为x=-1,
设A($\frac{{m}^{2}}{4}$,m),B($\frac{{n}^{2}}{4}$,n),(m>0,n<0),
由$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{9}{4}$,可得$\frac{(mn)^{2}}{16}$+mn=$\frac{9}{4}$,
解得mn=-18,
由题意可得C(-1,m),D(-1,n),
即有$\overrightarrow{OC}$•$\overrightarrow{OD}$=1+mn=1-18=-17.
故答案为:-17.
点评 本题考查向量的数量积的坐标表示,考查抛物线的方程和准线方程的运用,注意运用设而不求法,属于中档题.

练习册系列答案
相关题目
12.下列函数中,既在区间($\frac{3π}{2}$,2π)上是减函数,又是以π为周期的奇函数为( )
| A. | y=$\frac{1}{2}$sin4x | B. | y=sin2x-cos2x | C. | y=tan($\frac{π}{2}$-x) | D. | y=cos(2x+$\frac{π}{2}$) |
5.将函数y=f(x)cosx的图象向左平移$\frac{π}{4}$个单位后,得到函数y=2cos2x-1的图象,则f(x)=( )
| A. | 2sinx | B. | 2cosx | C. | -2sinx | D. | -2cosx |
12.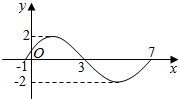 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )| A. | 2sin($\frac{x}{4}$-$\frac{π}{4}$) | B. | 2sin($\frac{x}{4}$+$\frac{π}{4}$) | C. | 2sin($\frac{πx}{4}$-$\frac{π}{4}$) | D. | 2sin($\frac{πx}{4}$+$\frac{π}{4}$) |
9.某几何体的三视图如图所示,则此几何体的体积等于( )
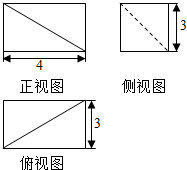

| A. | 45 | B. | 36 | C. | 30 | D. | 6 |
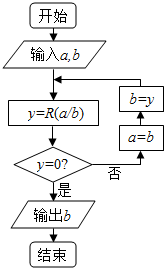 “辗转相除法”的算法思路如右图所示.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出b的值为( )
“辗转相除法”的算法思路如右图所示.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为243,45,则输出b的值为( )