题目内容
4.在[-3,3]上随机地取一个数b,则事件“直线y=x+b与圆x2+y2-2y-1=0有公共点”发生的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{4}$ |
分析 利用圆心到直线的距离小于等于半径可得到直线与圆有公共点,可求出满足条件的b,最后根据几何概型的概率公式可求出在[-3,3]上随机地取一个数b,事件“直线y=x+b与圆x2+y2-2y-1=0有公共点”发生的概率.
解答 解:圆x2+y2-2y-1=0的圆心为(0,1),半径为$\sqrt{2}$
圆心到直线y=x+b的距离为$\frac{|b-1|}{\sqrt{2}}$,
要使直线y=x+b与圆x2+y2-2y-1=0有公共点,
则$\frac{|b-1|}{\sqrt{2}}$$≤\sqrt{2}$,∴-1≤b≤3
∴在[-3,3]上随机地取一个数b,事件“直线y=x+b与圆x2+y2-2y-1=0有公共点”发生的概率为$\frac{3+1}{3+3}$=$\frac{2}{3}$,
故选A.
点评 本题主要考查了几何概型的概率,以及直线与圆相交的性质,解题的关键弄清概率类型,同时考查了计算能力.

练习册系列答案
相关题目
19.如图中的网格纸是边长为1的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为( )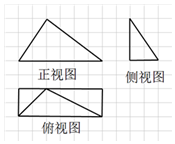

| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
9.如图所示某公司的组织结构图,信息部被( )直接领导


| A. | 专家办公室 | B. | 开发部 | C. | 总工程师 | D. | 总经理 |
13.设曲线y=eax-ln(x+1)在x=0处的切线方程为2x-y+1=0,则a=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.下列推理正确的是( )
| A. | 如果不买彩票,那么就不能中奖,因为你买了彩票,所以你一定中奖 | |
| B. | 因为a>b,a>c,所以a-b>a-c | |
| C. | 若a,b均为正实数,则lga+lgb≥2$\sqrt{lga•lgb}$ | |
| D. | 若ab<0,则$\frac{a}{b}$+$\frac{b}{a}$=-[(-$\frac{a}{b}$)+(-$\frac{b}{a}$)]≤-2$\sqrt{(-\frac{a}{b})(-\frac{b}{a})}$≤-2 |