题目内容
16.已知圆C的圆心在直线x+y+1=0,半径为5,且圆C经过点P(-2,0)和点Q(5,1).(1)求圆C的标准方程;
(2)求过点A(-3,0)且与圆C相切的切线方程.
分析 (1)根据条件利用待定系数法求出圆心即可求圆C的标准方程;
(2)根据直线和圆相切的等价条件即可求过点A(-3,0)且与圆C相切的切线方程.
解答 解:(1)设圆C:(x-a)2+(y-b)2=25,点C在直线x+y+1=0上,则有a+b+1=0,圆C经过点P(-2,0)和点Q(5,1),即:$\left\{\begin{array}{l}{(-2-a)^2}+{(0-b)^2}=25\\{(5-a)^2}+{(1-b)^2}=25\end{array}\right.$,解得:a=2,b=-3.
所以,圆C:(x-2)2+(y+3)2=25. …(5分)
(2)①若直线l的斜率不存在,即直线是x=-3,与圆相切,符合题意.…(7分)
②若直线l斜率存在,设直线l为y=k(x+3),即kx-y+3k=0.
由题意知,圆心C(2,-3)到直线l的距离等于半径5,即:$\frac{{|{2k+3+3k}|}}{{\sqrt{{k^2}+1}}}=5$(9分)
解得$k=\frac{8}{15}$,切线方程是$y=\frac{8}{15}(x+3)$. …(11分)
所求切线方程是x=-3或$y=\frac{8}{15}(x+3)$.…(12分)
点评 本题主要考查圆的方程的求解以及直线和圆相切的位置关系的应用,利用待定系数法是解决本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.如图是一个程序框图的一部分,若开始输入的数字为t=10,则输出的结果是( )


| A. | 20 | B. | 50 | C. | 140 | D. | 150 |
4.在[-3,3]上随机地取一个数b,则事件“直线y=x+b与圆x2+y2-2y-1=0有公共点”发生的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{4}$ |
1.已知集合A={-2,0,2},B={x|x2+x-2=0},则A∩B=( )
| A. | ∅ | B. | {2} | C. | {0} | D. | {-2} |
5. 如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )
如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )
 如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )
如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )| A. | π | B. | 2π | C. | 3π | D. | 4π |
6.已知f(x+y)=f(x)+f(y)且f(1)=2,则f(1)+f(2)+…+f(n)不能等于( )
| A. | f(1)+2f(1)+…+nf(1) | B. | f($\frac{n(n+1)}{2}$) | C. | n(n+1) | D. | n(n+1)f(1) |
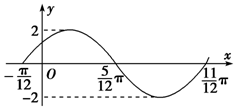 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的一段图象如图所示.
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的一段图象如图所示.