题目内容
 如图所示,在正方体ABCD-A′B′C′D′中,′E为DD′的中点,BD′为正方体的对角线,
如图所示,在正方体ABCD-A′B′C′D′中,′E为DD′的中点,BD′为正方体的对角线,(1)求证:BD′∥平面ACE;
(2)设正方体的棱长为a,沿着平面ACE将正方体截去一个棱锥D-ACE,求剩下的几何体的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连接BD,交AC于O,由已知得OE∥BD′,由此能证明BD′∥平面ACE.
(2)截去的几何体为三棱锥,以△ADC为底面,则DE为三棱锥的高,求出正方体的体积和截去的三棱锥的体积,由此能求出剩下的几何体的体积.
(2)截去的几何体为三棱锥,以△ADC为底面,则DE为三棱锥的高,求出正方体的体积和截去的三棱锥的体积,由此能求出剩下的几何体的体积.
解答:
(1)证明:连接BD,交AC于O,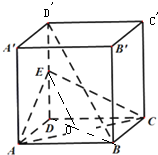
在△ACE中,E,O分别为DD′和AC的中点,
∴OE∥BD′,
又∵BD′不包含于平面ACE,OE?平面ACE,
∴BD′∥平面ACE.
(2)解:截去的几何体为三棱锥,若以△ADC为底面,则DE为三棱锥的高,
∵正方体的棱长为a,∴正方体的体积为V1=a3,
截去的三棱锥的体积V2=
Sh=
•
a2•
a=
a3,
∴剩下的几何体的体积V3=V1-V2=a3-
a3=
a3.

在△ACE中,E,O分别为DD′和AC的中点,
∴OE∥BD′,
又∵BD′不包含于平面ACE,OE?平面ACE,
∴BD′∥平面ACE.
(2)解:截去的几何体为三棱锥,若以△ADC为底面,则DE为三棱锥的高,
∵正方体的棱长为a,∴正方体的体积为V1=a3,
截去的三棱锥的体积V2=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
∴剩下的几何体的体积V3=V1-V2=a3-
| 1 |
| 12 |
| 11 |
| 12 |
点评:本题考查直线与平面平行的证明,考查几何体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图所示,AB和AC分别是圆O的切线,其中B,C切点,且OC=3,AB=4,延长AO与圆O交于点D,则△ABD的面积是
如图所示,AB和AC分别是圆O的切线,其中B,C切点,且OC=3,AB=4,延长AO与圆O交于点D,则△ABD的面积是 在△ABC中,AB=AC,D是△ABC外接圆AC上的一点,AE⊥BD于E,求证BE=CD+DE.
在△ABC中,AB=AC,D是△ABC外接圆AC上的一点,AE⊥BD于E,求证BE=CD+DE. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,BC∥AD,∠ABC=90°,AB=BC=PA=1,AD=2,E,F分别为PA,AD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,BC∥AD,∠ABC=90°,AB=BC=PA=1,AD=2,E,F分别为PA,AD的中点.