题目内容
1.若定义域均为D的三个函数f(x),g(x),h(x)满足条件:?x∈D,点(x,g(x)) 与点(x,h(x))都关于点(x,f(x))对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)=$\sqrt{1-{x}^{2}}$,f(x)=3x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是( )| A. | (-∞,-$\sqrt{10}$] | B. | [-$\sqrt{10}$,$\sqrt{10}$] | C. | [-3,$\sqrt{10}$] | D. | [$\sqrt{10}$,+∞) |
分析 根据对称函数的定义,结合h(x)≥g(x)恒成立,转化为点到直线的距离d≥1,利用点到直线的距离公式进行求解即可.
解答  解:∵x∈D,点(x,g(x)) 与点(x,h(x))都关于点(x,f(x))对称,
解:∵x∈D,点(x,g(x)) 与点(x,h(x))都关于点(x,f(x))对称,
∴$\frac{g(x)+h(x)}{2}$=f(x),
即2f(x)=g(x)+h(x)
∵h(x)≥g(x)恒成立,
∴2f(x)=g(x)+h(x)≥g(x)+g(x)=2g(x),
即f(x)≥g(x)恒成立,
作出g(x)和f(x)的图象,
若h(x)≥g(x)恒成立,
则h(x)在直线f(x)的上方,
即g(x)在直线f(x)的下方,
则直线f(x)的截距b>0,且原点到直线y=3x+b的距离d≥1,
即d=$\frac{|0-0+b|}{\sqrt{{3}^{2}+1}}$=$\frac{|b|}{\sqrt{10}}$≥1,即|b|≥$\sqrt{10}$,
则b≥$\sqrt{10}$或b≤-$\sqrt{10}$(舍),
即实数b的取值范围是[$\sqrt{10}$,+∞),
故选:D
点评 本题主要考查不等式恒成立问题,根据对称函数的定义转化为点到直线的距离关系,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
12.已知实数集R,集合A={x|x<0或x>2},集合B={y|y=$\sqrt{x-1}$},则(∁RA)∩B=( )
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
9.设集合A={x|x2-3x>0},B={x||x|<2},则A∩B=( )
| A. | (-2,0) | B. | (-2,3) | C. | (0,2) | D. | (2,3) |
13.甲、乙两人在5次体育测试中成绩见下表,其中●表示一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$.
| 甲 | 89 | 91 | 90 | 88 | 92 |
| 乙 | 83 | 87 | 9● | 83 | 99 |
11.设f(x)=(2x-1)ex,则f′(0)等于( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
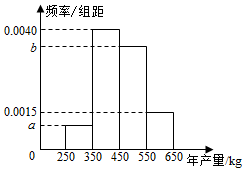 某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.