题目内容
19.函数$f(x)={log_2}x-(\frac{1}{2}{)^x}$的零点个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 可判断函数$f(x)={log_2}x-(\frac{1}{2}{)^x}$在其定义域上单调递增且连续,从而结合零点的判定定理应用.
解答 解:可判断函数$f(x)={log_2}x-(\frac{1}{2}{)^x}$在其定义域上单调递增且连续,
而f(1)=0-$\frac{1}{2}$<0,f(2)=1-$\frac{1}{4}$>0,
故f(x)在(1,2)上有零点,
故函数$f(x)={log_2}x-(\frac{1}{2}{)^x}$有且只有一个零点,
故选:A.
点评 本题考查了函数的性质的判断与应用,同时考查了零点的判定定理的应用.

练习册系列答案
相关题目
7.已知命题p:?x∈(0,$\frac{π}{2}$),使得cosx≥x,则该命题的否定是( )
| A. | ?x∈(0,$\frac{π}{2}$),使得cosx>x | B. | ?x∈(0,$\frac{π}{2}$),使得cosx≥x | ||
| C. | ?x∈(0,$\frac{π}{2}$),使得cosx<x | D. | ?x∈(0,$\frac{π}{2}$),使得cosx<x |
4.$sin\frac{2015π}{3}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
11.球O半径为R=13,球面上有三点A、B、C,AB=12$\sqrt{3}$,AC=BC=12,则四面体OABC的体积是( )
| A. | 60$\sqrt{3}$ | B. | 50$\sqrt{3}$ | C. | 60$\sqrt{6}$ | D. | 50$\sqrt{6}$ |
8.直线x=1的倾斜角是( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 不存在 |
9.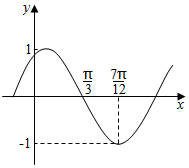 函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )
 函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)其中的图象如图所示,为了得到g(x)=cos(2x-$\frac{π}{2}$)的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
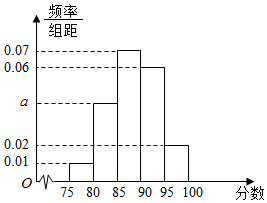 某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].
某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].