题目内容
9.若△ABC的内角A,C,B成等差数列,且△ABC的面积为2$\sqrt{3}$,则AB边的最小值是2$\sqrt{2}$.分析 由条件利用等差数列的定义求得C=$\frac{π}{3}$,再利用三角形的面积公式求得ab=8,再利用余弦定理,基本不等式即可求得AB边的最小值.
解答 解:△ABC中,A、C、B成等差数列,故2C=A+B,故C=$\frac{π}{3}$,A+B=$\frac{2π}{3}$.
∵△ABC的面积为$\frac{1}{2}$•ab•sinC=$\frac{1}{2}×ab×\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴ab=8,
∴AB2=c2=a2+b2-2abcosC=a2+b2-ab≥2ab-ab=ab=8,(当且仅当a=b时等号成立),
∴AB边的最小值为2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查等差数列的定义,三角形的面积公式,余弦定理,基本不等式在解三角形中的应用,考查了转化思想的应用,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
1.某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
(Ⅰ)写出价格f(x)关于时间x的函数关系式(x表示投放市场的第x天,x∈N*);
(Ⅱ)销售量g(x)与时间x的函数关系式为$g(x)=-\frac{1}{3}x+\frac{109}{3}({1≤x≤100,x∈{N^*}})$,则该产品投放市场第几天的销售额最高?最高为多少千元?
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
(Ⅱ)销售量g(x)与时间x的函数关系式为$g(x)=-\frac{1}{3}x+\frac{109}{3}({1≤x≤100,x∈{N^*}})$,则该产品投放市场第几天的销售额最高?最高为多少千元?
19.设Sn为等比数列{an}的前n项和,且8a2+a5=0,则S3:S2的值为( )
| A. | -3 | B. | 5 | C. | -8 | D. | -11 |
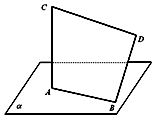 如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.
如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.