题目内容

求函数y=
2-cosx
sinx
在（0，π）上的最小值．
考点：三角函数的最值
专题：导数的综合应用
分析：利用导数研究函数的单调性极值与最值即可得出．
解答： 解：y′=f′（x）=
sin2x-(2-cosx)cosx
sin2x
=
1-2cosx
sin2x
，
当x∈(0，
π
3
)时，f′（x）＜0，函数f（x）在此区间上单调递减；当x∈(
π
3
，π)时，f′（x）＞0，函数f（x）在此区间上单调递增．
∴当x=
π
3
时，函数f（x）取得极小值即最小值，f(
π
3
)=
2-cos
π
3
sin
π
3
=
3
．
∴函数y=
2-cosx
sinx
在（0，π）上的最小值为
3
．
点评：本题考查了利用导数研究函数的单调性极值与最值，属于基础题．
练习册系列答案
相关题目
某校共有学生2000名，各年级男、女生人数如右表．已知在全校学生中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全校抽取80名学生，则应在三年抽取的学生人数为（　　）
一年级 二年级 三年级
女生 373 x y
男生 377 370 z
A、30B、25C、24D、20
设实数x，y满足
x-y-2≤0
x+2y-5≥0
y-2≤0
则z=
2x+y+2
x+1
的取值范围是（　　）
A、[
9
4
，3]
B、[
1
4
，1]
C、[1，
9
4
]
D、[1，3]
已知两个非零向量
m
=（
3
sinωx，cosωx），
n
=（cosωx，cosωx），ω＞0．
（Ⅰ）当ω=2，x∈（0，π）时，向量
m
与
n
共线，求x的值；
（Ⅱ）若函数f（x）=
m
•
n
的图象与直线y=
1
2
的任意两个相交邻点间的距离都是
π
2
，当f（
α
2
+
π
24
）=
1
2
+
2
6
，α∈（0，π）时，求cos2α的值．
在△ABC中，∠A，∠B，∠C所对的边分别是a、b、c，不等式x2cosC+4xsinC+6≥0对一切实数x恒成立．
（1）求cosC的取值范围；
（2）当∠C取最大值，且△ABC的周长为6时，求△ABC面积的最大值，并指出面积取最大值时△ABC的形状．
已知向量
a
=（2，1），
b
=（-1，1），
c
=（1，2）
（1）证明：（-
3
2
a
+
c
）∥（2
b
-
a
）
（2）若向量满足（
d
-
c
）⊥（
a
+
b
），且|
d
-
c
|=
5
，求
d
．
过O极点引直线交圆ρ2+r2-2rρcosθ-a2=0（r＞a＞0）于P，Q两点，在此直线上取一点R，使得
2
OR
=
1
OP
+
1
OQ
，求R点的轨迹的极坐标方程（r，a是常数）．
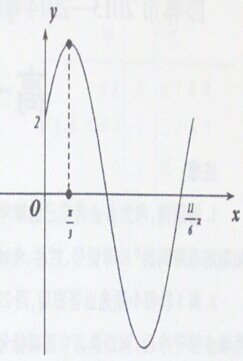已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜
π
2
）的部分图象如图所示．
（1）求f（x）的解析式；
（2）将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的
1
2
倍，再将所得函数图象向右平移
π
4
个单位，得到函数y=g（x）的图象，求g（x）的单调递减区间．
（Ⅰ）已知函数f（x）=|x-1|，解不等式f（x）+x2-1＞0；
（Ⅱ）已知函数f（x）=|x+2|-|x-1|，解不等式f（x）≥5x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网