题目内容
设α,β,γ是三个不重合的平面,l是直线,则下列结论正确的是( )
| A、若α⊥β,β⊥γ,则α⊥γ |
| B、若l⊥α,l?β,则α⊥β |
| C、若α∥β,且l∥α,则l∥β |
| D、若l上存在两点到α的距离相等,则l∥α |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:若α⊥β,β⊥γ,则α与γ相交或平行.故A错误;
若l⊥α,l?β,则由平面与平面垂直的判定定理得α⊥β,故B正确;
若α∥β,且l∥α,则l∥β或l?β,故C错误;
若l上存在两点到α的距离相等,则l∥α或l与α相交,故D错误.
故选:B.
若l⊥α,l?β,则由平面与平面垂直的判定定理得α⊥β,故B正确;
若α∥β,且l∥α,则l∥β或l?β,故C错误;
若l上存在两点到α的距离相等,则l∥α或l与α相交,故D错误.
故选:B.
点评:本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若平面向量
与
=(1,-2)的夹角是180°,且|
|=3
,则
等于( )
| a |
| b |
| a |
| 5 |
| a |
| A、.(6,-3) |
| B、(3,-6) |
| C、(-3,6) |
| D、(-6,3) |
将5件不同奖品全部奖给3个学生,每人至少一件奖品,则不同的获奖情况种数是( )
| A、150 | B、210 |
| C、240 | D、300 |
点M与定点F(4,0)的距离和它到定直线x=
的距离之比是常数
,则M的轨迹方程为( )
| 25 |
| 4 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果等差数列{an}中,a3+a4+a5=12,那么a4等于( )
| A、4 | B、2 | C、6 | D、12 |
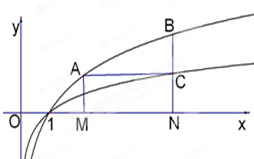 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点c,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点c,且AC与x轴平行.