题目内容
9.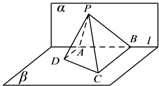 如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD,PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD,PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
分析 ∠PBA为所求的二面角的平面角,由△DAP∽△CPB得出$\frac{PA}{PB}=\frac{DA}{BC}=\frac{1}{2}$.求出P在α内的轨迹,根据轨迹的特点求出∠PBA的最大值对于的余弦值.
解答 解:∵AD⊥l,α∩β=l,α⊥β,AD?β,
∴AD⊥α,同理:BC⊥α.
∴∠DPA为直线PD与平面α所成的角,∠CPB为直线PC与平面α所成的角,
∴∠DPA=∠CPB,又∠DAP=∠CBP=90°,
∴△DAP∽△CPB,
∴$\frac{PA}{PB}=\frac{DA}{BC}=\frac{1}{2}$.
在平面α内,以AB为x轴,以AB的中垂线为y轴建立平面直角坐标系,
则A(-3,0),B(3,0).设P(x,y),(y>0)
∴2$\sqrt{(x+3)^{2}+{y}^{2}}$=$\sqrt{(x-3)^{2}+{y}^{2}}$,整理得(x+5)2+y2=16.
∴P点在平面α内的轨迹为以M(-5,0)为圆心,以4为半径的上半圆.
∵平面PBC∩平面β=BC,PB⊥BC,AB⊥BC,
∴∠PBA为二面角P-BC-D的平面角.
∴当PB与圆相切时,∠PBA最大,cos∠PBA取得最小值.
此时PM=4,MB=8,MP⊥PB,∴PB=4$\sqrt{3}$.
cos∠PBA=$\frac{PB}{MB}=\frac{4\sqrt{3}}{8}=\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了二面角的计算,

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
19.使不等式2x-4>0成立的一个充分不必要条件是( )
| A. | x>2 | B. | x>3 | C. | x>1 | D. | x∈{1,2} |
18.在平行四边形ABCD中,O是对角线的交点,$\overrightarrow{CE}$=-3$\overrightarrow{DE}$,则( )
| A. | $\overrightarrow{OE}$=-$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\overrightarrow{OE}$=-$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AD}$ | C. | $\overrightarrow{OE}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{4}$$\overrightarrow{AD}$ | D. | $\overrightarrow{OE}$=$\frac{1}{4}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AD}$ |