题目内容
17.设函数$f(x)=\sqrt{1-x}+\sqrt{1+x}$.(1)求函数f(x)的值域;
(2)当实数x∈[0,1],证明:$f(x)≤2-\frac{1}{4}{x^2}$.
分析 (1)由已知条件可以推知$f'(x)=\frac{{\sqrt{1-x}-\sqrt{1+x}}}{{2\sqrt{1-{x^2}}}}$,结合该函数的单调性求解;
(2)把证明不等式成立问题转化为判断函数单调性问题解决,利用(1)的结论即可得出结论.
解答 解:(1)由题意知,函数f(x)的定义域是[-1,1],
∵$f'(x)=\frac{{\sqrt{1-x}-\sqrt{1+x}}}{{2\sqrt{1-{x^2}}}}$,当f'(x)≥0时,解得x≤0,
∴f(x)在(0,1)上单调递减,在(-1,0)上单调递增,
∴$f{(x)_{min}}=f(1)=f(-1)=\sqrt{2}$,f(x)max=f(0)=2,
∴函数f(x)的值域为$[\sqrt{2},2]$.
(2)设$h(x)=\sqrt{1-x}+\sqrt{1+x}+\frac{1}{4}{x^2}-2$,x∈[0,1],h(0)=0,
∵$h'(x)=-\frac{1}{2}{(1-x)^{-\frac{1}{2}}}+\frac{1}{2}{(1+x)^{-\frac{1}{2}}}+\frac{1}{2}x$,=$\frac{1}{2}x[1-\frac{2}{{\sqrt{1-{x^2}}(\sqrt{1+x}+\sqrt{1-x})}}]$,
∵$\sqrt{1-{x^2}}(\sqrt{1+x}+\sqrt{1-x})$=$\sqrt{1-{x^2}}•\sqrt{2+2\sqrt{1-{x^2}}}≤2$,
∴h'(x)≤0.
∴h(x)在(0,1)上单调递减,又h(0)=0,
∴$f(x)≤2-\frac{1}{4}{x^2}$.
点评 本题主要考查函数单调性的判断及证明不等式恒成立问题,考查利用导数研究函数的性质,逻辑性强,属难题.

| A. | $\frac{1}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
| A. | 命题“?x0∈R+,x02-x0<0”的否定是“?x∈R-,x2-x≥0” | |
| B. | 命题“若a≠b,则a2≠b2”的否命题是“若a≠b,则a2=b2” | |
| C. | x1>1且x2>1的充要条件是x1+x2>2. | |
| D. | p,q为两个命题,若p∨q为真且p∧q为假,则p,q两个命题中必有一个为真,一个为假. |
| A. | 1-3i | B. | 1+3i | C. | -1+3i | D. | -1-3i |
| A. | M(5,7) | B. | M(4,5) | C. | M(2,1) | D. | M(2,3) |
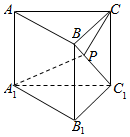 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面A1B1C1,且A1C1⊥B1C1,A1C1=3$\sqrt{2}$,B1C1=CC1=2,P是BC1上一动点,则CP+PA1的最小值为( )| A. | 5$\sqrt{2}$ | B. | 5 | C. | $\sqrt{10}$ | D. | $\sqrt{34}$ |
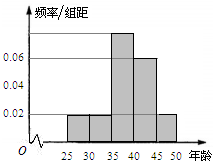 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.(Ⅰ)求正整数a,b,N的值;
(Ⅱ)现要从年龄低于40岁的员工用分层抽样的方法抽取42人,则年龄在第1,2,3组得员工人数分别是多少?
(Ⅲ)为了估计该单位员工的阅读倾向,现对该单位所有员工中按性别比例抽查的40人是否喜欢阅读国学类书
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 14 | 4 | 18 |
| 女 | 8 | 14 | 22 |
| 合计 | 22 | 18 | 40 |
下面是年龄的分布表:
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
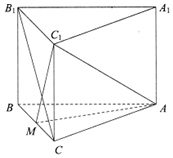 在三棱柱ABC-A1B1C1中,已知侧棱CC1⊥底面ABC,M为BC的中点,$AC=AB=3,BC=2,C{C_1}=\sqrt{2}$.
在三棱柱ABC-A1B1C1中,已知侧棱CC1⊥底面ABC,M为BC的中点,$AC=AB=3,BC=2,C{C_1}=\sqrt{2}$.