题目内容
2.直线MN的斜率为2,其中点N(1,-1),点M在直线y=x+1上,则( )| A. | M(5,7) | B. | M(4,5) | C. | M(2,1) | D. | M(2,3) |
分析 设M的坐标为(a,b),根据题意可得b=a+1①,$\frac{b+1}{a-1}$=2②,联立①②解可得a=4,b=5,即可得答案.
解答 解:根据题意,设M的坐标为(a,b),
若点M在直线y=x+1上,则有b=a+1,①
若直线MN的斜率为2,则有$\frac{b+1}{a-1}$=2,②
联立①②解可得a=4,b=5,
即M的坐标为(4,5);
故选:B.
点评 本题考查直线的斜率计算,关键是掌握直线的斜率计算公式.

练习册系列答案
相关题目
13.若θ是第二象限角且sinθ=$\frac{12}{13}$,则$tan(θ+\frac{π}{4})$=( )
| A. | $-\frac{17}{7}$ | B. | $-\frac{7}{17}$ | C. | $\frac{17}{7}$ | D. | $\frac{7}{17}$ |
10.中国古代数学著作《张丘建算经》(成书约公元5世纪)卷上二十三“织女问题”:今有女善织,日益功疾.初日织五尺,今一月日织九匹三丈.问日益几何.其意思为:有一个女子很会织布,一天比一天织得快,而且每天增加的长度都是一样的.已知第一天织5尺,经过一个月30天后,共织布九匹三丈.问每天多织布多少尺?
(注:1匹=4丈,1丈=10尺).此问题的答案为( )
(注:1匹=4丈,1丈=10尺).此问题的答案为( )
| A. | 390尺 | B. | $\frac{16}{31}$尺 | C. | $\frac{16}{29}$尺 | D. | $\frac{13}{29}$尺 |
7.函数f(x)=sin(ωx+φ)(x∈R,ω>0,-π≤φ<π)的部分图象如图所示,则( )
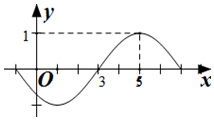

| A. | ω=$\frac{π}{2}$,φ=-π | B. | ω=$\frac{π}{2}$,φ=0 | C. | ω=$\frac{π}{4}$,φ=$\frac{π}{4}$ | D. | ω=$\frac{π}{4}$,φ=-$\frac{3π}{4}$ |
12.已知函数:①y=x3+3x2;②$y=\frac{{{e^x}+{e^{-x}}}}{2}$;③$y={log_2}\frac{3-x}{3+x}$;④y=xsinx,从中任取两个函数,则这两函数奇偶性相同的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |