题目内容
已知a为正整数，且关于x的方程lg（4-2x2）=lg（a-x）+1有实根，则a等于（ ）
| A、1 | B、1或2 | C、2 | D、2或3 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：依题意，可得x2-5x+（5a-2）=0，由△≥0即可求得a的值．
解答：
解：∵lg（4-2x2）=lg（a-x）+1，
∴lg（4-2x2）=lg10（a-x），
∴
，
由4-2x2=10（a-x），得x2-5x+（5a-2）=0，
依题意，△=25-4（5a-2）=32-20a≥0，
∴a≤
，又a为正整数，
∴a=1．
故选：A．
∴lg（4-2x2）=lg10（a-x），
∴
|
由4-2x2=10（a-x），得x2-5x+（5a-2）=0，
依题意，△=25-4（5a-2）=32-20a≥0，
∴a≤
| 8 |
| 5 |
∴a=1．
故选：A．
点评：本题考查根的存在性及根的个数判断，着重考查等价转化思想与解方程的能力，属于中档题．
练习册系列答案
相关题目
一个酒杯的截面是抛物线的一部分，其方程x2=2y（0≤y≤20），杯内放入一个球，要使球触及杯底部，则球的半径的取值范围为（ ）
| A、（0，1] | ||||
B、（0，
| ||||
C、（0，
| ||||
D、（0，
|
设全集U=R，函数y=lg（2-x）的定义域为A，集合B={x|1＜x＜3}，则（∁UA）∩B等于（ ）
| A、[2，3） |
| B、（1，2） |
| C、（2，3） |
| D、[1，2） |
已知向量
=（m，n），
=（1，-1），其中m，n∈{1，2，3，4，5}，则
与
的夹角能成为直角三角形内角的概率是（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若sin（
-θ）=
，则cos（
+2θ）的值为（ ）
| π |
| 6 |
| 1 |
| 3 |
| 2π |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若框图所给的程序运行结果为V=10，那么判断框中可以填入的关于n的条件是（ ）
| A、n＜19？ |
| B、n≤19？ |
| C、n＜18？ |
| D、n≤18？ |
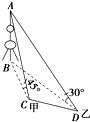要测量底部不能到达的东方明珠电视塔的高度，在黄浦江西岸选择甲、乙两观测点，在甲、乙两点测得塔顶的仰角分别为45°、30°，在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°，甲、乙两地相距500米，则电视塔在这次测量中的高度是（ ）