题目内容
函数f（x）=
的单调区间是 ．
| ||
| cos x |
考点：函数的单调性及单调区间
专题：函数的性质及应用
分析：根据f（x）=
=
，分sinx＞0 和sinx＜0两种情况，分别化简函数的解析式，根据正切函数的图象特征，求出f（x）的单调区间．
| ||
| cos x |
| |sinx| |
| cosx |
解答：
解：函数f（x）=
=
，
①当x∈[2kπ，2kπ+π]，k∈z时，sinx＞0，f（x）=tanx，
故函数的增区间为[2kπ，2kπ+
）、（2kπ+
，2kπ+π]，k∈z．
②当x∈（2kπ+π，2kπ+2π]，k∈z时，sinx＜0，f（x）=-tanx，
故函数的减区间为（2kπ+π，2kπ+
）、（2kπ+
，2kπ+2π]，k∈z．
故函数的增区间为：[2kπ，2kπ+
）、（2kπ+
，2kπ+π]；减区间为 （2kπ+π，2kπ+
）、（2kπ+
，2kπ+2π]，k∈z，
故答案为：增区间为：[2kπ，2kπ+
）、（2kπ+
，2kπ+π]；减区间为 （2kπ+π，2kπ+
）、（2kπ+
，2kπ+2π]，k∈z．
| ||
| cos x |
| |sinx| |
| cosx |
①当x∈[2kπ，2kπ+π]，k∈z时，sinx＞0，f（x）=tanx，
故函数的增区间为[2kπ，2kπ+
| π |
| 2 |
| π |
| 2 |
②当x∈（2kπ+π，2kπ+2π]，k∈z时，sinx＜0，f（x）=-tanx，
故函数的减区间为（2kπ+π，2kπ+
| 3π |
| 2 |
| 3π |
| 2 |
故函数的增区间为：[2kπ，2kπ+
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
故答案为：增区间为：[2kπ，2kπ+
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
点评：本题主要考查正切函数的图象特征，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
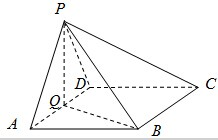如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，Q为AD的中点．