题目内容
已知(1-2x)7=a0+a1x+a2x2+a7x7.求|ai|(其中i=1,2,…,7)的最大值.
考点:二项式系数的性质
专题:二项式定理
分析:根据(1-2x)7 的展开式的通项公式为Tr+1=
•(-2)r•xr,求得|ai|=|
•(-2)i|,由此可得当r=5时,|ai|取得最大值为672.
| C | r 7 |
| C | i 7 |
解答:
解:∵(1-2x)7=a0+a1x+a2x2+a7x7 ,(1-2x)7 的展开式的通项公式为Tr+1=
•(-2)r•xr,
故有|ai|=|
•(-2)i|,i=0,1,2,3,4,5,6,7,检验可得当r=5时,|ai|取得最大值为672.
| C | r 7 |
故有|ai|=|
| C | i 7 |
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
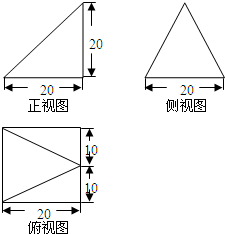 已知某个几何体的三视图如图,根据图中标出 的尺寸(单位:cm),则此几何体的所有侧面的面积中最大的是( )
已知某个几何体的三视图如图,根据图中标出 的尺寸(单位:cm),则此几何体的所有侧面的面积中最大的是( )A、100
| ||
B、100
| ||
C、200
| ||
D、200
|

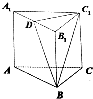 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,∠ACB=90°,D是AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,∠ACB=90°,D是AA1的中点.