题目内容
 如图,矩形ABCD所在的平面与平面ABF互相垂直,在△ABF中,AB=
如图,矩形ABCD所在的平面与平面ABF互相垂直,在△ABF中,AB=| 3 |
(1)求证:AB⊥CF;
(2)若四棱锥F-ABCD的体积为1,求直线OP与平面ABF所成角的大小.
考点:直线与平面所成的角,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)首先,证明AB⊥BF,然后,AB⊥CB,从而得到AB⊥平面CFB,故得到该命题成立;
(2)首先,找到∠CFB为直线CF与平面ABF所成的角,然后,在三角形中求解即可.
(2)首先,找到∠CFB为直线CF与平面ABF所成的角,然后,在三角形中求解即可.
解答:
解:(1)在△ABF中,AB=
,AF=2,BF=1,
∴AB2+BF2=AF2,
∴AB⊥BF,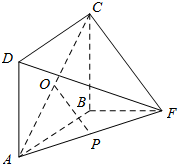
而矩形ABCD中AB⊥CB,
∴AB⊥平面CFB,
又∵CF?平面BCF∵AB⊥CF,
(2)∵VF-ABCD=
S矩形ABCD•BF=
×BC×
×1=1
∴BC=
,
∵CB⊥平面ABF,
∴∠CFB为直线CF与平面ABF所成的角,
在Rt△ABC中,BF=1,
∴tan∠CFB=
=
,
∴∠CFB=60°,
又∵O、P分别为AC和AF的中点,
∴OP∥CF,
∴直线OP与平面ABF所成角的大小等于直线CF与平面ABF所成角的大小,
∴直线OP与平面ABF所成角为60°.
| 3 |
∴AB2+BF2=AF2,
∴AB⊥BF,

而矩形ABCD中AB⊥CB,
∴AB⊥平面CFB,
又∵CF?平面BCF∵AB⊥CF,
(2)∵VF-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
∴BC=
| 3 |
∵CB⊥平面ABF,
∴∠CFB为直线CF与平面ABF所成的角,
在Rt△ABC中,BF=1,
∴tan∠CFB=
| BC |
| BF |
| 3 |
∴∠CFB=60°,
又∵O、P分别为AC和AF的中点,
∴OP∥CF,
∴直线OP与平面ABF所成角的大小等于直线CF与平面ABF所成角的大小,
∴直线OP与平面ABF所成角为60°.
点评:本题综合考查了空间中直线与直线平行和垂直、线面角、线面垂直的判定和性质定理等知识,属于综合性题目,处理求解空间角问题时,解决的总的思路是:先找,后求的原则.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
甲、乙、丙、丁等六人站成一排,要求甲、乙均不与丙相邻且丁必须排在首位,则不同的排法种数为( )
| A、72种 | B、52种 |
| C、36种 | D、24种 |
 一个几何体的三视图如图所示,主视图与侧视图都是边长为
一个几何体的三视图如图所示,主视图与侧视图都是边长为2的正三角形,俯视图为正方形,则该几何体的全面积为( )
| A、4 | ||
| B、8 | ||
| C、12 | ||
D、4+4
|
实数x,y满足条件
,则22x-y的最小值为( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、4 |
 高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.
高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.