题目内容
9.若集合A={0,1,2,x},B={1,x2},A∪B=A,则满足条件的实数x有2个.分析 由A∪B=A说明B是A的子集,然后利用子集的概念分类讨论x的取值.
解答 解:由A∪B=A,所以B⊆A.
又A={0,1,2,x},B={1,x2},
所以x2=0,或x2=2,或x2=x.
x2=0时,集合A违背元素的互异性,所以x2≠0.
x2=2时,x=-$\sqrt{2}$或x=$\sqrt{2}$.符合题意.
x2=x时,得x=0或x=1,集合A均违背元素互异性,所以x2≠x.
所以满足条件的实数x的个数有2个.
故答案是:2.
点评 本题考查了并集及其运算,考查了子集的概念,考查了集合中元素的特性,解答的关键是要考虑集合中元素的互异性,是基本的概念题,也是易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知直线 2x+my-1=0与直线 3x-2y+n=0垂直,垂足为 (2,p),则m+n+p=( )
| A. | -6 | B. | 6 | C. | 4 | D. | 10 |
19.在等比数列{an}中,若an>0,a7=2,则$\frac{1}{a_3}+\frac{2}{{{a_{11}}}}$的最小值为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 4 | D. | 8 |
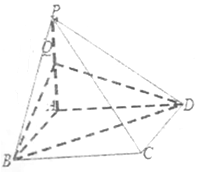 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.