题目内容
19.如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=60°,且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,则双曲线的离心率为$\frac{\sqrt{7}}{2}$.分析 确定△QAP为等边三角形,设AQ=2R,则OP=R,利用勾股定理,结合余弦定理,即可得出结论
解答 解:因为∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,
所以△QAP为等边三角形,
设AQ=2R,则OP=R,
渐近线方程为y=$\frac{b}{a}$x,A(a,0),取PQ的中点M,则AM=$\frac{|-ab|}{\sqrt{{a}^{2}+{b}^{2}}}$
由勾股定理可得(2R)2-R2=($\frac{|-ab|}{\sqrt{{a}^{2}+{b}^{2}}}$)2,
所以(ab)2=3R2(a2+b2)①
在△OQA中,$\frac{(3R)^{2}+(2R)^{2}-{a}^{2}}{2×3R×2R}$=$\frac{1}{2}$,所以7R2=a2②
①②结合c2=a2+b2,可得e=$\frac{c}{a}$=$\frac{\sqrt{7}}{2}$.
故答案为:$\frac{{\sqrt{7}}}{2}$
点评 本题考查双曲线的性质,考查余弦定理、勾股定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
14.函数$f(x)=cos(3x+\frac{5π}{2})$,满足$\frac{f({x}_{i})}{{x}_{i}}=m$,其中${x}_{i}∈[-2π,2π],i=1,2,…,n,n∈{N}^{*}$,则n的最大值为( )
| A. | 13 | B. | 12 | C. | 10 | D. | 8 |
11.已知$\frac{π}{2}$<α<π,3sin2α=2cosα,则cos(π-α)的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
8.已知点O是锐角△ABC的外心,a,b,c分别为内角A、B、C的对边,A=$\frac{π}{4}$,且$\frac{cosB}{sinC}$$\overrightarrow{AB}$+$\frac{cosC}{sinB}$$\overrightarrow{AC}$=λ$\overrightarrow{OA}$,则λ的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | -$\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
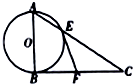 如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.