题目内容
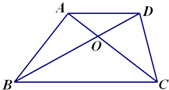如图：在梯形ABCD中，AD∥BC且AD=| 1 |
| 2 |
| AB |
| a |
| AD |
| b |
| a |
| b |
| BO |
| BO |
考点：平面向量的基本定理及其意义
专题：计算题,平面向量及应用
分析：先化简
=
-
=
-
；从而得到
=x
=x（
-
）；同理可得（1-x）
+x
=y（
+2
）；从而解得．
| BD |
| AD |
| AB |
| b |
| a |
| BO |
| BD |
| b |
| a |
| a |
| b |
| a |
| b |
解答：
解：由题意，
=
-
=
-
；
∵O，B，D三点共线，
∴
=x
=x（
-
）；
=
+
=
+x（
-
）=（1-x）
+x
；
=
+
=
+2
；
则由A，O，C三点共线知，
（1-x）
+x
=y（
+2
）；
故
；
解得x=
，y=
；
故
=
（
-
）=-
+
；
故答案为：-
+
．
| BD |
| AD |
| AB |
| b |
| a |
∵O，B，D三点共线，
∴
| BO |
| BD |
| b |
| a |
| AO |
| AB |
| BO |
| a |
| b |
| a |
| a |
| b |
| AC |
| AB |
| BC |
| a |
| b |
则由A，O，C三点共线知，
（1-x）
| a |
| b |
| a |
| b |
故
|
解得x=
| 2 |
| 3 |
| 1 |
| 3 |
故
| BO |
| 2 |
| 3 |
| b |
| a |
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
故答案为：-
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
点评：本题考查了平面向量的应用，属于基础题．
练习册系列答案
相关题目
已知集合，则A={{1，2，3，4，5，6}，B={y|y=
，x∈A}，则 A∩B=（ ）
| x |
| A、{1，2} |
| B、{1，2，3} |
| C、{1，3，5} |
| D、{1，2，3，4，5，6} |
已知点P（2，y）在抛物线y2=4x上，则P点到焦点F的距离为（ ）
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|