题目内容
7.已知数列{an}为等比数列,且a1a13+2a72=5π,则cos(a2a12)的值为( )| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
分析 利用等比数列通项公式求出${a}_{2}{a}_{12}={{a}_{7}}^{2}$=$\frac{5π}{3}$,由此能求出cos(a2a12)的值.
解答 解:∵数列{an}为等比数列,且a1a13+2a72=5π,
∴a1a13+2a72=3a72=5π,∴${{a}_{7}}^{2}$=$\frac{5π}{3}$,
${a}_{2}{a}_{12}={{a}_{7}}^{2}$=$\frac{5π}{3}$,
∴cos(a2a12)=cos$\frac{5π}{3}$=cos(2$π-\frac{π}{3}$)=cos$\frac{π}{3}$=$\frac{1}{2}$.
故选:D.
点评 本题考查等比数列的通项公式、余弦函数、诱导公式等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是基础题.

练习册系列答案
相关题目
13.已知抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l于点Q,M,N分别为PQ,PF的中点,MN与x轴相交于点R,若∠NRF=60°,则|FR|等于( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
12.在△ABC中,D,E分别为BC,AB的中点,F为AD的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=-1$,AB=2AC=2,则$\overrightarrow{CE}•\overrightarrow{AF}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{4}$ |
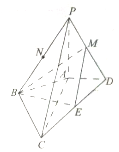 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N分别为PD,PB,CD的中点.