题目内容
已知在正项数列{an}中,Sn表示数列{an}前n项和且Sn=
an2+
an+
,n∈N+,数列{bn}满足bn=
,Tn为数列{bn}的前n项和.
(I) 求an,Sn;
(Ⅱ)是否存在最大的整数t,使得对任意的正整数n均有Tn>
总成立?若存在,求出t;若不存在,请说明理由.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4Sn-1 |
(I) 求an,Sn;
(Ⅱ)是否存在最大的整数t,使得对任意的正整数n均有Tn>
| t |
| 36 |
考点:数列与不等式的综合
专题:
分析:(Ⅰ)由条件再写一式,两式相减,从而数列{an}是首项为1,公差为2的等差数列,由此能求出an,Sn.
(Ⅱ)由(Ⅰ)知bn=
=
(
-
),Tn=
[(1-
)+(
-
)+…(
-
)]=
(1-
)=
,由此能求出t=11符合题意.
(Ⅱ)由(Ⅰ)知bn=
| 1 |
| 4Sn-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
解答:
解:(Ⅰ)∵Sn=
an2+
an+
,∴当n=1时,S1=a1=
a12+
a1+
得a1=1,…(1分)
当n≥2时,an=Sn-Sn-1=(
an2+
an+
)-(
a
+
an-1+
)
整理得(an+an-1)(an-an-1-2)=0…(3分)
∵数列{an}各项为正,
∴an+an-1>0…(4分)
∴an-an-1=2…(5分)
∴数列{an}是首项为1,公差为2的等差数列
∴an=a1+(n-1)×2=2n-1.…(6分)
∴Sn=
=n2…(7分)
(Ⅱ)由(Ⅰ)知bn=
=
(
-
) …(8分)
于是Tn=
[(1-
)+(
-
)+…(
-
)]=
(1-
)=
…(10分)
易知数列{Tn}是递增数列,故T1=
是最小值,…(12分)
所以只需
>
,即t<12,因此存在t=11符合题意.…(14分)
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
当n≥2时,an=Sn-Sn-1=(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
2 n-1 |
| 1 |
| 2 |
| 1 |
| 4 |
整理得(an+an-1)(an-an-1-2)=0…(3分)
∵数列{an}各项为正,
∴an+an-1>0…(4分)
∴an-an-1=2…(5分)
∴数列{an}是首项为1,公差为2的等差数列
∴an=a1+(n-1)×2=2n-1.…(6分)
∴Sn=
| n[1+(2n-1)] |
| 2 |
(Ⅱ)由(Ⅰ)知bn=
| 1 |
| 4Sn-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
于是Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
易知数列{Tn}是递增数列,故T1=
| 1 |
| 3 |
所以只需
| 1 |
| 3 |
| t |
| 36 |
点评:本题考查数列的通项公式和前n项和公式的合理运用,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
已知椭圆C1、C2的离心率分别为e1、e2,若椭圆C1比C2更圆,则e1与e2的大小关系正确的是( )
| A、e1<e2 |
| B、e1=e2 |
| C、e1>e2 |
| D、e1、e2大小不确定 |
已知不等式-2xy≤ax2+2y2,若对任意x∈[1,2]及y∈[-1,3]不等式恒成立,则实数a的范围是( )
A、0≤a≤
| ||
| B、a≥0 | ||
C、a≥
| ||
D、a≥-
|
定义在R上的偶函数f(x),满足f(x+2)=f(x),且在区间[-1,0]上为递增,则( )
A、f(
| ||
B、f(2)<f(3)<f(
| ||
C、f(3)<f(2)<f(
| ||
D、f(3)<f(
|
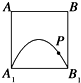
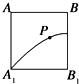
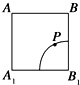
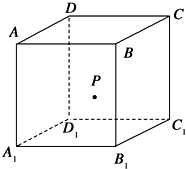 如图正方体A1B1C1D1-ABCD的侧面AB1内有动点P到直线AB与到直线B1C1的距离相等,则动点P所在的曲线的形状为 ( )
如图正方体A1B1C1D1-ABCD的侧面AB1内有动点P到直线AB与到直线B1C1的距离相等,则动点P所在的曲线的形状为 ( )
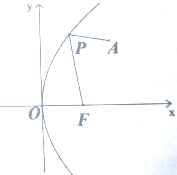 如图,F是抛物线C:y2=2px的焦点,点A(4,2)为抛物线于内一点,点P为抛物线上一动点,|PA|+|PF|的最小值为8
如图,F是抛物线C:y2=2px的焦点,点A(4,2)为抛物线于内一点,点P为抛物线上一动点,|PA|+|PF|的最小值为8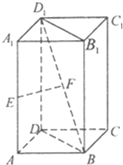 如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.
如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.