题目内容
6.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{|x-1|}}&{x>0}\\{-{x}^{2}-2x+1}&{x≤0}\end{array}\right.$,若关于x的方程f2(x)+(a-1)f(x)=a有7个不等的实数根,则实数a的取值范围是(-2,-1).分析 画出函数的图象,f(x)=1时有3个不等的实数根,f(x)=-a时,有4个不等的实数根,利用函数的图象,求解a的范围.
解答 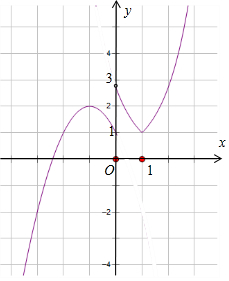 解:函数f(x)=$\left\{\begin{array}{l}{{3}^{|x-1|}}&{x>0}\\{-{x}^{2}-2x+1}&{x≤0}\end{array}\right.$,的图象如图:
解:函数f(x)=$\left\{\begin{array}{l}{{3}^{|x-1|}}&{x>0}\\{-{x}^{2}-2x+1}&{x≤0}\end{array}\right.$,的图象如图:
关于x的方程f2(x)+(a-1)f(x)=a,即f(x)=-a或f(x)=1
f(x)=1时有3个不等的实数根,f(x)=-a时,有4个不等的实数根,
由函数f(x)图象,可得-a∈(1,2),
∴a∈(-2,-1).
故答案为(-2,-1).
点评 本题考查函数与方程的应用,函数的零点个数的判断与应用,考查数形结合以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.我市正在建设最具幸福感城市,原计划沿渭河修建7个河滩主题公园.为提升城市品位、升级公园功能,打算减少2个河滩主题公园,两端河滩主题公园不在调整计划之列,相邻的两个河滩主题公园不能同时被调整,则调整方案的种数为( )
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
11.命题“y=f(x)(x∈M)是奇函数”的否定是( )
| A. | ?x∈M,f(-x)=-f(x) | B. | ?x∈M,f(-x)≠-f(x) | C. | ?x∈M,f(-x)=-f(x) | D. | ?x∈M,f(-x)≠-f(x) |
18.已知直线y=2x-3与抛物线y2=4x交于A,B两点,O为坐标原点,OA,OB的斜率分别为k1,k2,则$\frac{1}{k_1}+\frac{1}{k_2}$( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{3}$ |
16.已知集合A={x∈N|x-2≤0},集合B={x|x2-x-2<0},则A∩B=( )
| A. | {1,2} | B. | {0,1} | C. | {0,1,2} | D. | {-1,0,1,2} |