题目内容
在极坐标系中，圆ρ2-4ρcosθ+3=0上的动点P到直线θ=
（ρ∈R）的距离最小值是 ．
| π |
| 3 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：圆ρ2-4ρcosθ+3=0化为x2+y2-4x+3=0，可得圆心C（2，0），半径r=1．直线θ=
（ρ∈R）化为y=
x．利用点到直线的距离公式可得：圆心C到直线的距离d，即可得出圆ρ2-4ρcosθ+3=0上的动点P到直线θ=
（ρ∈R）的距离最小值=d-r．
| π |
| 3 |
| 3 |
| π |
| 3 |
解答：
解：圆ρ2-4ρcosθ+3=0化为x2+y2-4x+3=0，配方为（x-2）2+y2=1，可得圆心C（2，0），半径r=1．
直线θ=
（ρ∈R）化为y=
x．
∴圆心C到直线的距离d=
=
，
∴圆ρ2-4ρcosθ+3=0上的动点P到直线θ=
（ρ∈R）的距离最小值=d-r=
-1．
故答案为：
-1．
直线θ=
| π |
| 3 |
| 3 |
∴圆心C到直线的距离d=
2
| ||||
|
| 3 |
∴圆ρ2-4ρcosθ+3=0上的动点P到直线θ=
| π |
| 3 |
| 3 |
故答案为：
| 3 |
点评：本题考查了极坐标方程化为直角坐标方程、点到直线的距离公式、圆上的点到直线的距离，考查了计算能力，属于基础题．
练习册系列答案
相关题目
甲、乙两人在一次射击比赛中各射靶5次．两人成绩的统计表如甲表、乙表所示，则：（ ）
甲表：
乙表：
甲表：
| 环数 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 1 | 1 | 1 | 1 | 1 |
| 环数 | 5 | 6 | 9 |
| 频数 | 3 | 1 | 1 |
| A、甲成绩的平均数小于乙成绩的平均数 |
| B、甲成绩的中位数小于乙成绩的中位数 |
| C、甲成绩的方差小于乙成绩的方差 |
| D、甲成绩的极差小于乙成绩的极差 |
命题“?x0∈R，使得2x0≤4”的否定是（ ）
| A、?x∈R，使得2x＞4 |
| B、?x0∈R，使得2x0≥4 |
| C、?x∈R，使得2x＜4 |
| D、?x0∈R，使得2x0＞4 |
已知两点A（1，0），B（-1，
），O为坐标原点，点C在第二象限，且∠AOC=135°，设
=-
+λ
（λ∈R），则实数λ等于（ ）
| 3 |
| OC |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
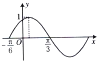函数f（x）=sin（ωx+φ）（x∈R）（ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
与圆x2+（y+5）2=9相切，且在两坐标轴上截距相等的直线共有（ ）条．
| A、2 | B、3 | C、4 | D、6 |
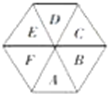在一个正六边形的六个区域栽种观赏植物（如图），要求同一块中种同一种植物，相邻的两块种不同的植物．