题目内容
3.已知函数fn(x)=$\frac{1}{3}$x3-$\frac{1}{2}$(n+1)x2+x(n∈N*)数列{an}满足an+1=fn′(an),a1=3.(1)求a2,a3,a4;
(2)根据(1)猜想数列{an}的通项公式,并用数学归纳法证明;
(3)求证:对一切正整数n,$\frac{1}{{{{({a_1}-2)}^2}}}+\frac{1}{{{{({a_2}-2)}^2}}}+\frac{1}{{{{({a_3}-2)}^2}}}+…+\frac{1}{{{{({a_n}-2)}^2}}}<\frac{7}{4}$.
分析 (1)由求导公式和法则求出fn′(x),由an+1=fn′(an)和a1=3求出a2,依次求出a3和a4;
(2)由(1)猜想得an=n+2,利用数学归纳法证明成立;
(3)由(2)求出an-2,对n=1、2时代入数据证明不等式成立,当n≥3时时先化简不等式的左边,再利用放缩法和裂项求和法证明不等式成立.
解答 解:(1)由题意得,fn′(x)=x2-(n+1)x+1 (1分)
∵an+1=fn′(an),a1=3,
∴a2=f1′(a1)=a12-2a1+1=4,(2分)
a3=f2′(a2)=a22-3a2+1=5,(3分)
a4=f3′(a3)=a32-4a3+1=6;(4分)
(2)猜想an=n+2,用数学归纳法证明:
①当n=1时,a1=1+2=3显然成立.(5分)
②假设当n=k(k∈N+)时猜想成立,
则n=k(k∈N+)时,ak=k+2,(6分)
则当n=k+(k∈N+)时,
ak+1=fk′(ak)=ak2-(k+1)ak+1=(k+2)2-(k+1)(k+2)+1
=k+3=(k+1)+2
∴当n=k+1时,猜想成立 (8分)
由①②可知对一切n∈N+,an=n+2成立 (9分)
(3)由(2)得,an-2=(n+2)-2=n,
当n=1时,$\frac{1}{{{{({a_1}-2)}^2}}}=\frac{1}{1^2}=1<\frac{7}{4}$;(10分)
当n=2时,$\frac{1}{{{{({a_1}-2)}^2}}}+\frac{1}{{{{({a_2}-2)}^2}}}$=1+$\frac{1}{4}$=$\frac{5}{4}<\frac{7}{4}$;(11分)
当n≥3时,$\frac{1}{{{{({a_1}-2)}^2}}}+\frac{1}{{{{({a_2}-2)}^2}}}+\frac{1}{{{{({a_3}-2)}^2}}}+…+\frac{1}{{{{({a_n}-2)}^2}}}$
=$1+\frac{1}{4}+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}+…+\frac{1}{{n}^{2}}$<$1+\frac{1}{4}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{(n-1)n}$
=$1+\frac{1}{4}+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{n-1}-\frac{1}{n})$
=1+$\frac{1}{4}$+$\frac{1}{2}$-$\frac{1}{n}$=$\frac{7}{4}$-$\frac{1}{n}$<$\frac{7}{4}$,
综上,对一切正整数n有结论成立.(14分)
点评 本题考查了数列的递推公式,数列求和方法:裂项求和法,求导公式和法则,以及数学归纳法,放缩法证明不等式的综合应用,考查化简、变形能力.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,其焦点与椭圆上最近点的距离为2-$\sqrt{2}$.
在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,其焦点与椭圆上最近点的距离为2-$\sqrt{2}$.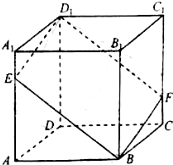 已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④
已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④