题目内容
2．数列{an}满足$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{3}$+$\frac{{a}_{3}}{5}$+…+$\frac{{a}_{n}}{2n-1}$=3n+1，则数列{an}的通项公式为an=（2n-1）•2•3n．分析 利用方程组法，两式相减可求数列{an}的通项公式．
解答 解：数列{an}满足$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{3}$+$\frac{{a}_{3}}{5}$+…+$\frac{{a}_{n}}{2n-1}$=3n+1…①
则有：$\frac{{a}_{1}}{1}$+$\frac{{a}_{2}}{3}$+$\frac{{a}_{3}}{5}$+…+$\frac{{a}_{n-1}}{2（n-1）-1}$=3n…②，
由①-②可得：$\frac{{a}_{n}}{2n-1}$=3n+1-3n=2•3n
∴an=（2n-1）•2•3n
故答案为：（2n-1）•2•3n
点评 本题主要考查数列通项公式的求解，构造了方程组，加减消项法，属于基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
9．有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表．
已知在全部105人中随机抽取一人为优秀的概率为$\frac{2}{7}$．
（1）请完成上面的列联表；
（2）根据列联表的数据，若按97.5%的可靠性要求，能否认为“成绩与班级有关系”；
（3）若按下面的方法从甲班优秀的学生抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到8或9号的概率．
参考公式和数据：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 105 |
（1）请完成上面的列联表；
（2）根据列联表的数据，若按97.5%的可靠性要求，能否认为“成绩与班级有关系”；
（3）若按下面的方法从甲班优秀的学生抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到8或9号的概率．
参考公式和数据：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17．抛掷两枚骰子，当至少有一枚5点或6点出现时，就说试验成功，则在30次独立重复试验中成功的次数X的数学期望是（ ）
| A． | $\frac{40}{3}$ | B． | $\frac{50}{3}$ | C． | 10 | D． | 20 |
7．
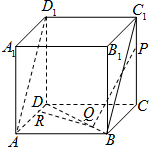如图，在棱长为1的正方体ABCD-A1B1C1D1中，P、Q分别是线段CC1，BD上的点，R是直线AD上的点，满足PQ∥平面ABC1D1，PQ⊥RQ，则|PR|的最小值是（ ）
如图，在棱长为1的正方体ABCD-A1B1C1D1中，P、Q分别是线段CC1，BD上的点，R是直线AD上的点，满足PQ∥平面ABC1D1，PQ⊥RQ，则|PR|的最小值是（ ）| A． | $\frac{\sqrt{42}}{6}$ | B． | $\frac{\sqrt{30}}{5}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，其焦点与椭圆上最近点的距离为2-$\sqrt{2}$．