题目内容
已知M={x|x2≤4},N={x|
≥1},则M∩N=( )
| 2 |
| x-1 |
| A、{x|1<x≤2} |
| B、{x|-2≤x≤1} |
| C、{x|1≤x≤2} |
| D、{x|x<2} |
考点:交集及其运算
专题:集合
分析:由M={x|x2≤4}={x|-2≤x≤2},N={x|
≥1}={x|1<x≤3},能求出M∩N.
| 2 |
| x-1 |
解答:
解:∵M={x|x2≤4}={x|-2≤x≤2},
N={x|
≥1}={x|1<x≤3},
∴M∩N={x|1<x≤2}.
故选:A.
N={x|
| 2 |
| x-1 |
∴M∩N={x|1<x≤2}.
故选:A.
点评:本题考查交集的求法,是基础题,解题时要认真审题,注意交集性质的合理运用.

练习册系列答案
相关题目
“m<1”是“函数f(x)=x2-x+
m存在零点”的( )
| 1 |
| 4 |
| A、充分不必要条件 |
| B、充要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
执行如图所示的程序框图,输出的S值为( )


| A、250-1 | ||
| B、251-1 | ||
C、
| ||
D、
|
已知5555=8k+m,(k,m∈N*),则整数m可以为( )
| A、1 | B、2 | C、6 | D、7 |
曲线
(θ为参数)的焦距是( )
|
| A、2 | B、5 | C、8 | D、10 |
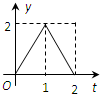
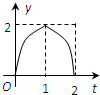
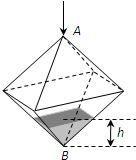 如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )
如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )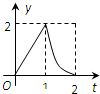
 如图,以椭圆C:
如图,以椭圆C: