题目内容
若(1+3x)n的展开式中,二项式系数之和为an,各项系数之和为bn,则
的值为 .
| lim |
| n→+∞ |
| an-bn |
| an+3bn |
考点:二项式系数的性质
专题:二项式定理
分析:由题意可得an=2n,bn=4n,再根据则
=
=
=
,利用函数极限的运算法则计算求得结果.
| lim |
| n→+∞ |
| an-bn |
| an+3bn |
| lim |
| n→+∞ |
| 2n-4n |
| 2n+3•4n |
| lim |
| n→+∞ |
| 1-2n |
| 1+3•2n |
| lim |
| n→+∞ |
| ||
|
解答:
解:由题意可得an=2n,在(1+3x)n的展开式中,令x=1可得各项系数之和为bn=4n,
则
=
=
=
=
=-
,
故答案为:-
.
则
| lim |
| n→+∞ |
| an-bn |
| an+3bn |
| lim |
| n→+∞ |
| 2n-4n |
| 2n+3•4n |
| lim |
| n→+∞ |
| 1-2n |
| 1+3•2n |
| lim |
| n→+∞ |
| ||
|
| 0-1 |
| 0+3 |
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入.还考查了函数极限的运算法则的应用,属于基题.

练习册系列答案
相关题目
下列语句是命题的有( )
| A、x2-3≥x |
| B、与一条直线相交的两直线平行吗? |
| C、?x∈Z,3x+1=5x |
| D、好难的题目! |
已知M={x|x2≤4},N={x|
≥1},则M∩N=( )
| 2 |
| x-1 |
| A、{x|1<x≤2} |
| B、{x|-2≤x≤1} |
| C、{x|1≤x≤2} |
| D、{x|x<2} |
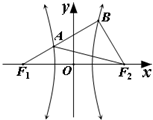 如图,F1、F2是双曲线
如图,F1、F2是双曲线