Question

如图在棱长为1的正方体ABCD-A₁B₁C₁D₁中，点E为棱BC的中点，点F是棱CD上的动点．
（1）试确定F点的位置，使得D₁E⊥平面AB₁F；
（2）当D₁E⊥平面AB₁F时，求二面角C₁-EF-C的余弦值．

Answer 1

考点：用空间向量求平面间的夹角,直线与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）建立空间直角坐标系，利用向量法能求出F为棱CD上的中点．
（2）求出平面C₁EF的法向量和平面CEF的法向量，利用向量法能求出二面角C₁-EF-C的余弦值．

解答： 解：（1）建立如图所示的空间直角坐标系，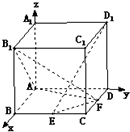
则A（0，0，0），B₁（1，0，1），
F（x，1，0），E（1，

1

2

，0，D₁（0，1，1），

AB1

=（1，0，1），

AF

=（x，1，0），

EB1

=（-1，

1

2

，1），
∵D₁E⊥面AB₁F，∴

ED1

•

AB1

=0，

ED1

•

AF

=0，
∴-x+

1

2

=0，解得x=

1

2

，
∴F为棱CD上的中点．
（2）

EC1

=（0，

1

2

，1），

FC1

=（

1

2

，0，1），
设平面C₁EF的一个法向量为

n

=（x，y，z），
则

n • EC1 =0 n • FC1 =0

，∴

1 2 y+z=0 1 2 x+z=0

，取z=-1，得

n

=（2，2，-1），
而平面CEF的一个法向量为

CC1

=（0，0，1），
∴cos＜

n

，

CC1

＞=

-1

3

=-

1

3

，
∵二面角C₁-EF-C是锐二面角，
∴二面角C₁-EF-C的余弦值为

1

3

．

点评：本题考查点的位置的确定，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．