题目内容
如果函数y=f（x）的图象关于y轴对称，且f（x）=（x-2008）2+1（x≥0），则f（x）（x＜0）的表达式为 ．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：函数y=f（x）的图象关于y轴对称，所以该函数时偶函数，则可以设x＜0，然后-x＞0，代入f（x）当x＞0时的解析式，结合奇偶性求出x＜0时的f（x），则问题可解．
解答：
解；由题意函数f（x）的图象关于y轴对称，所以该函数是偶函数，
所以f（-x）=f（x），设x＜0，则-x＞0，又因为f（x）=（x-2008）2+1（x≥0）
所以f（x）=f（-x）=（-x-2008）2+1=（x+2008）2+1（x＜0）
故答案为：f（x）=（x+2008）2+1（x＜0）
所以f（-x）=f（x），设x＜0，则-x＞0，又因为f（x）=（x-2008）2+1（x≥0）
所以f（x）=f（-x）=（-x-2008）2+1=（x+2008）2+1（x＜0）
故答案为：f（x）=（x+2008）2+1（x＜0）
点评：本题考查了偶函数的几何性质，以及利用转化思想求解析式的方法．注意结果表达时勿忘定义域．
练习册系列答案
相关题目
下列各组对象构成集合的是（ ）
| A、2013年全国的本科毕业生 |
| B、2013中国小麦产量较高的城市 |
| C、著名数学家 |
| D、与无理数π无限接近的数 |
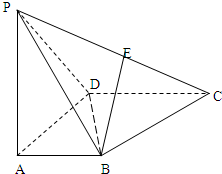四棱锥P-ABCD中，ABCD为平行四边形，PA⊥底面ABCD，∠BAC=30°，PA=BD，
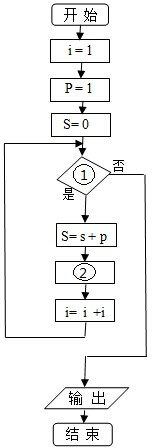给出50个数，1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推．要求计算这50个数的和．先将下面给出的程序框图补充完整，再根据程序框图写出程序．
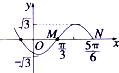已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象如图所示，若函数g（x）与函数f（x）的图象关于点P（