题目内容
在二项式(x-1)6的展开式中,含x3的项的系数是 .
考点:二项式系数的性质
专题:二项式定理
分析:利用二项式展开式的通项公式Tr+1,求出展开式中含x3的项的系数是什么.
解答:
解:在二项式(x-1)6的展开式中,
∵Tr+1=
•x6-r•(-1)r,
令6-r=3,
得r=3;
∴
•(-1)3=-20,
即含x3的项的系数是-20.
故答案为:-20.
∵Tr+1=
| C | r 6 |
令6-r=3,
得r=3;
∴
| C | 6-3 6 |
即含x3的项的系数是-20.
故答案为:-20.
点评:本题考查了二项式定理的应用问题,解题时应利用二项式展开式的通项公式Tr+1,进行解答计算,是基础题.

练习册系列答案
相关题目
6人站成一排,甲、乙、丙3个人不能都站在一起的排法种数为( )
| A、720 | B、144 |
| C、576 | D、684 |
已知i为虚数单位,复数z=
,则复数
在复平面上的对应点位于( )
| 1+2i |
| 1-i |
. |
| z |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
已知y=f(x)是R上的增函数,令F(x)=f(1-x)-f(3+x),则F(x)是R上的( )
| A、增函数 | B、减函数 |
| C、先增后减 | D、先减后增 |

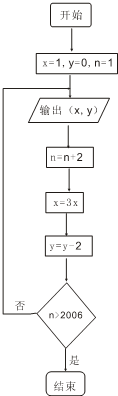 已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…
已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…