题目内容
11．若集合M={y|y=2x}，P={x|y=$\sqrt{x-1}$}，M∩P=（ ）| A． | [1，+∞） | B． | [0，+∞） | C． | （0，+∞） | D． | （1，+∞） |
分析 根据题意，写出集合M与P，由集合交集的意义即可得答案．
解答 解：根据题意，集合M为函数y=2x的值域，则M={y|y=2x}={y|y＞0}=（0，+∞），
集合P为函数y=$\sqrt{x-1}$的定义域，则P={x|y=$\sqrt{x-1}$}=[1，+∞），
则M∩P=[1，+∞），
故选：A．
点评 本题考查集合交集的运用，注意集合N的表示形式．
练习册系列答案
相关题目
2．已知$sin（-α）=\frac{{\sqrt{5}}}{3}$，则$cos（\frac{π}{2}+α）$的值为（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{{\sqrt{5}}}{3}$ | D． | $-\frac{{\sqrt{5}}}{3}$ |
19．某市电子认证审查流程图如图：
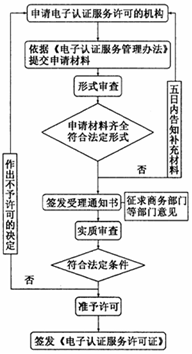
则有几处审查可能不被通过的环节（ ）
则有几处审查可能不被通过的环节（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 0 |
20．等差数列{an}中，a1=2，公差d=3则{an}的通项公式为（ ）
| A． | .an=3n-1 | B． | an=2n+1 | C． | .an=2n+3 | D． | .an=3n+2 |
1．已知函数f（x）=sinx-λcosx的图象的一个对称中心是（$\frac{π}{3}$，0），则函数g（x）=λsinxcosx+sin2x图象的一条对称轴是（ ）
| A． | x=-$\frac{π}{3}$ | B． | x=$\frac{2π}{3}$ | C． | x=$\frac{π}{6}$ | D． | x=$\frac{5π}{6}$ |