题目内容
17.在△ABC中,内角A,B,C所对的边分别为a,b,c,且a2-c2=2b,sinAcosC=3cosAsinC,则下列关于△ABC的表述中正确的是( )| A. | 必有一边等于4 | B. | 必有一边等于5 | ||
| C. | AC边上的高是一个定值 | D. | 不可能是钝角三角形 |
分析 由题意利用诱导公式,正弦定理和余弦定理,求得b=4,从而结合所给的选项得出结论.
解答 解:△ABC中,∵sinAcosC=3cosAsinC,∴sin(A+C)=4cosAsinC,
即 sinB=4cosAsinC,即b=4c•cosA=4c•$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$,∴b2=2a2-2c2.
再根据a2-c2=2b,可得b2=4b,∴b=4,
故选:A.
点评 本题主要考查诱导公式,正弦定理和余弦定理的应用,属于中档题.

练习册系列答案
相关题目
8.函数f(x)=2cos2(x+$\frac{π}{8}$)-2sin(x+$\frac{π}{8}$)cos(x+$\frac{π}{8}$)-1的最大值是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}$ |
2.将4个球随机放入3个空盒,则所有球都在两个盒中,但不是全在一个盒子里的概率为( )
| A. | $\frac{7}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{14}{27}$ | D. | $\frac{14}{81}$ |
7.若函数f(x)=x2log2(x+$\sqrt{x^2+m}$)为奇函数,则m=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
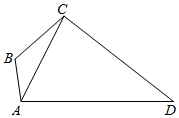 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.