题目内容
9.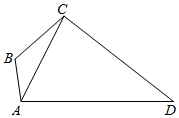 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.(Ⅰ)求sin∠BAC;
(Ⅱ)求DC的长.
分析 (I)在△ABC中使用正弦定理得出sin∠ACB,使用两角和的正弦函数公式求出;
(II)求出sin∠CAD,sinD,在△ACD中使用正弦定理解出CD.
解答 解:(I)在△ABC中,由正弦定理得$\frac{AB}{sin∠ACB}=\frac{AC}{sinB}$,即$\frac{1}{sin∠ACB}=\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}$,
解得sin∠ACB=$\frac{\sqrt{21}}{14}$.∴cos∠ACB=$\frac{5\sqrt{7}}{14}$,
∴sin∠BAC=sin($\frac{π}{3}-∠ACB$)=$\frac{\sqrt{3}}{2}$cos∠ACB-$\frac{1}{2}$sin∠ACB=$\frac{\sqrt{3}}{2}×\frac{5\sqrt{7}}{14}-\frac{1}{2}×\frac{\sqrt{21}}{14}$=$\frac{\sqrt{21}}{7}$.
(II)∵∠BAC+∠CAD=$\frac{π}{2}$,
∴sin∠CAD=cos∠BAC=$\frac{2\sqrt{7}}{7}$,cos∠CAD=sin∠BAC=$\frac{\sqrt{21}}{7}$.
∴sinD=sin($\frac{2π}{3}-∠CAD$)=$\frac{\sqrt{3}}{2}$cos∠CAD+$\frac{1}{2}$sin∠CAD=$\frac{\sqrt{3}}{2}×\frac{\sqrt{21}}{7}+\frac{1}{2}×\frac{2\sqrt{7}}{7}$=$\frac{5\sqrt{7}}{14}$.
在△ACD中,由正弦定理得$\frac{AC}{sinD}=\frac{CD}{sin∠CAD}$,即$\frac{\sqrt{7}}{\frac{5\sqrt{7}}{14}}=\frac{CD}{\frac{2\sqrt{7}}{7}}$,
解得CD=$\frac{4\sqrt{7}}{5}$.
点评 本题考查了正余弦定理在解三角形中的应用,选择恰当的三角形的元素是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题. | |
| B. | 命题p:$?{x_0}∈R,x_0^2-2{x_0}+4<0$,则$?p:?x∈R,x_{\;}^2-2{x_{\;}}+4≥0$ | |
| C. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 | |
| D. | “$φ=\frac{π}{2}$”是“y=cos(2x+φ)为奇函数”的充要条件 |
| A. | -$\frac{12}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
| A. | 必有一边等于4 | B. | 必有一边等于5 | ||
| C. | AC边上的高是一个定值 | D. | 不可能是钝角三角形 |
| A. | 0.6 | B. | 0.36 | C. | 0.24 | D. | 0.4 |
| A. | A∩B=∅ | B. | A∩C=∅ | C. | A∪C={1,2,3} | D. | A∪C={2,3} |
 如图,在四边形ABCD中,BC=1,DC=2,四个内角A,B,C,D的度数之比为3:7:4:10.求:
如图,在四边形ABCD中,BC=1,DC=2,四个内角A,B,C,D的度数之比为3:7:4:10.求: