题目内容

6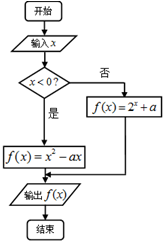．运行如图程序框图，若对任意输入的实数x，有f（x）≥a成立，且存在实数x0，使得f（x0）=a成立，则实数a的值为（　　）
A．-4B．0C．4D．-4或0

分析 题意等价于“已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}+a，x≥0}\\{{x}^{2}-ax，x＜0}\end{array}\right.$的最小值是a，求a的值．”分类讨论，利用函数的图象，即可得出结论．

解答 解：题意等价于“已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}+a，x≥0}\\{{x}^{2}-ax，x＜0}\end{array}\right.$的最小值是a，求a的值．”
当a≥0时，如图11（1），f（x）无最小值；
当a＜0时，如图11（2），f（x）最小值是f（$\frac{a}{2}$）=-$\frac{{a}^{2}}{4}$，
∴-$\frac{{a}^{2}}{4}$=a，
∴a=0（舍）或a=-4．
故选A．

点评 本题考查程序框图，考查数形结合的数学思想，正确运用函数的图象是关键．

练习册系列答案
相关题目
5．已知A={1，3，9，27，81}，B={y|y=log3x，x∈A}，则A∩B=（　　）
A．{1，3}B．{3，27，81}C．{1，3，9}D．{9，27}
17．已知函数$f（x）=\frac{x}{lnx}-ax$．
（1）a=1，x＞1时，求证：$f（x）•\frac{x-1}{x}＜\frac{3-x}{2}$；
（2）求证：$\sum_{k=1}^n{\frac{2}{2k+1}}≤\frac{2}{3}+ln\frac{n+1}{2}\;（n∈N，n≥2）$；
（3）若$?{x_1}，{x_2}∈[{e，{e^2}}]$，使f（x1）-f′（x2）≤a成立，求实数a的取值范围．
14．已知函数f（x）=lnx-$\frac{a}{x}$．
（1）当a＞0时，求f（x）在[e，+∞）上的最小值；
（2）若f（x）在[1，e]上的最小值为$\frac{3}{2}$，求实数a的值；
（3）若f（x）＜x2在（1，+∞）上恒成立，求a的取值范围．
1．已知函数f（x）=k（x+1）2-x，g（x）=2x-k•2-x（k∈R且k≠0）
（1）若f（1）=23，求函数g（x）在区间[0，1]上的值域；
（2）当-3＜g（1）＜3时，函数f（x）在区间[0，2]上的最小值大于h（x）=$\frac{2x}{{x}^{2}+1}$+$\frac{{x}^{2}+1}{x}$在（0，+∞]上的最小值，求实数k的取值范围．
11．已知抛物线Γ：y2=4x，点N（a，0），O为坐标原点，若在抛物线Γ上存在一点M，使得$\overrightarrow{OM}$•$\overrightarrow{NM}$=0，则实数a的取值范围是a＞4．
18．已知a=0.33，b=30.3，c=0.23，则a，b，c的大小关系为（　　）
A．a＜b＜cB．c＜a＜bC．b＜a＜cD．c＜b＜a
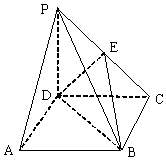15．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，E是PC的中点．
（1）证明：PA∥平面EDB；
（2）证明：BC⊥DE．
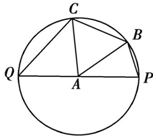16．已知PQ是半径为1的圆A的直径，B，C为不同于P，Q的两点，如图所示，记∠PAB=θ．
（1）若BC=$\sqrt{2}$，求四边形PBCQ的面积的最大值；
（2）若BC=1，求$\overrightarrow{BP}$•$\overrightarrow{CQ}$的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网