题目内容
15.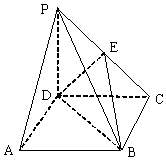 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.(1)证明:PA∥平面EDB;
(2)证明:BC⊥DE.
分析 (1)连结AC,AC交BD于O,连结EO,证明PA∥EO,然后证明PA∥平面EDB.
(2)证明PD⊥BC,DC⊥BC,推出BC⊥平面PDC.然后证明BC⊥DE.
解答 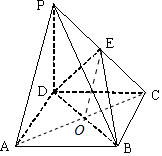 证明:(1)连结AC,AC交BD于O,连结EO.…(2分)
证明:(1)连结AC,AC交BD于O,连结EO.…(2分)
∵底面ABCD是正方形,∴点O是AC的中点
在△PAC中,EO是中位线,∴PA∥EO …(4分)
而EO?平面EDB且PA?平面EDB,
所以,PA∥平面EDB …(6分)
(2)∵PD⊥底面ABCD且BC?底面ABCD,∴PD⊥BC ①
又∵底面ABCD是正方形,有DC⊥BC ②
其中PD∩DC=D∴BC⊥平面PDC. …(10分)
又∵DE?平面PDC,∴BC⊥DE. …(12分)
点评 本题考查直线与平面平行于垂直的判定定理以及性质定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
6.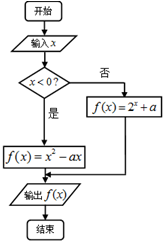 运行如图程序框图,若对任意输入的实数x,有f(x)≥a成立,且存在实数x0,使得f(x0)=a成立,则实数a的值为( )
运行如图程序框图,若对任意输入的实数x,有f(x)≥a成立,且存在实数x0,使得f(x0)=a成立,则实数a的值为( )
 运行如图程序框图,若对任意输入的实数x,有f(x)≥a成立,且存在实数x0,使得f(x0)=a成立,则实数a的值为( )
运行如图程序框图,若对任意输入的实数x,有f(x)≥a成立,且存在实数x0,使得f(x0)=a成立,则实数a的值为( )| A. | -4 | B. | 0 | C. | 4 | D. | -4或0 |
5.下列各组对象中不能构成集合的是( )
| A. | 蒙中高一(一)班的全体男生 | B. | 蒙中全校学生家长的全体 | ||
| C. | 李明的所有家人 | D. | 王明的所有好朋友 |