题目内容
16.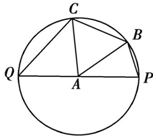 已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.
已知PQ是半径为1的圆A的直径,B,C为不同于P,Q的两点,如图所示,记∠PAB=θ.(1)若BC=$\sqrt{2}$,求四边形PBCQ的面积的最大值;
(2)若BC=1,求$\overrightarrow{BP}$•$\overrightarrow{CQ}$的最大值.
分析 (1)根据条件可得到$∠BAC=\frac{π}{2}$,进而得出$∠CAQ=\frac{π}{2}-θ$,由三角形面积公式即可求出${S}_{四边形PBCQ}=\frac{1}{2}sinθ+\frac{1}{2}cosθ+\frac{1}{2}$,由两角和的正弦公式即可得到${S}_{四边形PBCQ}=\frac{\sqrt{2}}{2}sin(θ+\frac{π}{4})+\frac{1}{2}$,从而求出四边形PBCQ的面积的最大值;
(2)由条件可得到$∠BAC=\frac{π}{3},∠PAC=\frac{π}{3}+θ$,而$\overrightarrow{BP}=\overrightarrow{AP}-\overrightarrow{AB},\overrightarrow{CQ}=\overrightarrow{AQ}-\overrightarrow{AC}$,代入$\overrightarrow{BP}•\overrightarrow{CQ}$进行数量积的运算,然后化简即可得出$\overrightarrow{BP}•\overrightarrow{CQ}=sin(θ+\frac{π}{6})-\frac{1}{2}$,从而得出该数量积的最大值.
解答 解:(1)∵$AB=AC=1,BC=\sqrt{2}$,∴∠BAC=$\frac{π}{2}$;
由∠PAB=θ得∠CAQ=$\frac{π}{2}-θ$;
∴S四边形PBCQ=S△PAB+S△ABC+S△CAQ
=$\frac{1}{2}sinθ+\frac{1}{2}+\frac{1}{2}sin(\frac{π}{2}-θ)$
=$\frac{1}{2}sinθ+\frac{1}{2}cosθ+\frac{1}{2}$
=$\frac{\sqrt{2}}{2}sin(θ+\frac{π}{4})+\frac{1}{2}$;
∵$0<θ<\frac{π}{2}$,∴当$θ=\frac{π}{4}$时,S四边形PBCQ取得最大值$\frac{{\sqrt{2}+1}}{2}$;
(2)当BC=1时,∠BAC=$\frac{π}{3}$,∠PAC=$\frac{π}{3}+θ$;
∴$\overrightarrow{BP}•\overrightarrow{CQ}=(\overrightarrow{AP}-\overrightarrow{AB})•(\overrightarrow{AQ}-\overrightarrow{AC})$
=$\overrightarrow{AP}•\overrightarrow{AQ}-\overrightarrow{AP}•\overrightarrow{AC}-\overrightarrow{AB}•\overrightarrow{AQ}+\overrightarrow{AB}•\overrightarrow{AC}$
=-1$-cos(\frac{π}{3}+θ)+cosθ+\frac{1}{2}$
=$-\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ+cosθ-\frac{1}{2}$
=$\frac{{\sqrt{3}}}{2}sinθ+\frac{1}{2}cosθ-\frac{1}{2}$
=$sin({θ+\frac{π}{6}})-\frac{1}{2}$;
∵$0<θ<\frac{2π}{3}$;
∴$θ=\frac{π}{3}$时,$\overrightarrow{BP}•\overrightarrow{CQ}$取得最大值$\frac{1}{2}$.
点评 考查三角形的面积公式,两角和的正余弦公式,三角函数的诱导公式,以及正弦函数的最值.

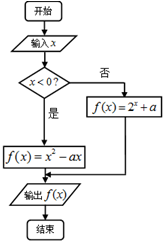 运行如图程序框图,若对任意输入的实数x,有f(x)≥a成立,且存在实数x0,使得f(x0)=a成立,则实数a的值为( )
运行如图程序框图,若对任意输入的实数x,有f(x)≥a成立,且存在实数x0,使得f(x0)=a成立,则实数a的值为( )| A. | -4 | B. | 0 | C. | 4 | D. | -4或0 |
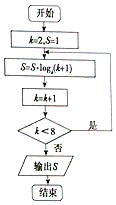
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
| A. | 蒙中高一(一)班的全体男生 | B. | 蒙中全校学生家长的全体 | ||
| C. | 李明的所有家人 | D. | 王明的所有好朋友 |