题目内容
16.z=a+2i(a∈R),若z2+8i为纯虚数,则a=2.分析 利用复数代数形式的乘除运算化简复数z2+8i,由其实部为0且虚部不为0求得a值.
解答 解:∵z=a+2i(a∈R),
∴z2+8i=(a+2i)2+8i=(a2-4)+(4a+8)i,
又z2+8i为纯虚数,
则$\left\{\begin{array}{l}{{a}^{2}-4=0}\\{4a+8≠0}\end{array}\right.$,解得a=2.
故答案为:2.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
4.如图,在矩形ABCD中,AB=2,AD=4,点E在线段AD上且AE=3,现分别沿BE,CE将△ABE,△DCE翻折,使得点D落在线段AE上,则此时二面角D-EC-B的余弦值为( )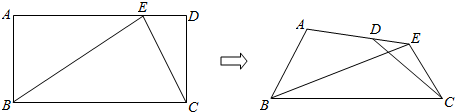

| A. | $\frac{4}{5}$ | B. | $\frac{5}{6}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
8.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$是两个不共线的向量,且向量m$\overrightarrow{a}$-3$\overrightarrow{b}$与$\overrightarrow{a}$+(2-m)$\overrightarrow{b}$共线,则实数m的值为( )
| A. | -1或3 | B. | $\sqrt{3}$ | C. | -1或4 | D. | 3或4 |
5.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}=2\sqrt{3}\overrightarrow{BD}$,$|{\overrightarrow{AD}}|=1$,则$\overrightarrow{AC}•\overrightarrow{AD}$=( )
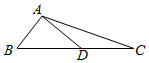

| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
6.下列式子中成立的是( )
| A. | log76<log67 | B. | 1.013.4>1.013.5 | C. | 3.50.3<3.40.3 | D. | log0.44<log0.46 |
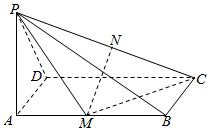 如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.
如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.