题目内容
15.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{25}$=1(a>5)的两个焦点为F1、F2,且|F1F2|=8.弦AB过点F1,则△ABF2的周长为( )| A. | 10 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
分析 求得椭圆的a,b,c,由椭圆的定义可得△ABF2的周长为|AB|+|AF2|+|BF2|=4a,计算即可得到所求值.
解答 解:由题意可得椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{25}$=1的b=5,c=4,
a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{41}$,
由椭圆的定义可得|AF1|+|AF2|=|BF1|+|BF2|=2a,
即有△ABF2的周长为|AB|+|AF2|+|BF2|
=|AF1|+|AF2|+|BF1|+|BF2|=4a=4$\sqrt{41}$.
故选:D..
点评 本题考查三角形的周长的求法,注意运用椭圆的定义和方程,定义法解题是关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图,在矩形ABCD中,AB=2,AD=4,点E在线段AD上且AE=3,现分别沿BE,CE将△ABE,△DCE翻折,使得点D落在线段AE上,则此时二面角D-EC-B的余弦值为( )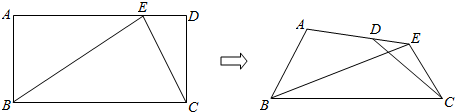

| A. | $\frac{4}{5}$ | B. | $\frac{5}{6}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
5.如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}=2\sqrt{3}\overrightarrow{BD}$,$|{\overrightarrow{AD}}|=1$,则$\overrightarrow{AC}•\overrightarrow{AD}$=( )
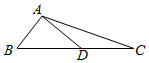

| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
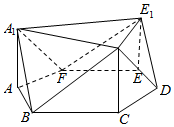 已知如图几何体A1C1E1-ABCDEF底面是边长为2的六变形,AA1,CC1,EE1长度为2且都垂直与底面,
已知如图几何体A1C1E1-ABCDEF底面是边长为2的六变形,AA1,CC1,EE1长度为2且都垂直与底面,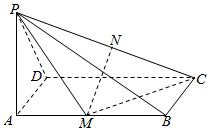 如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.
如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.