题目内容
19.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$过点A(2,3),且F(2,0)为其右焦点.(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在于行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于$\frac{10\sqrt{13}}{13}$?若存在,求出直线l的方程;若不存在,请说明理由.
分析 (Ⅰ)利用椭圆焦点和椭圆定义,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)设存在符合题意的直线l,其方程为y=$\frac{3}{2}x+t$,与椭圆联立,得3x2+3tx+t2-12=0,由此利用根的判别式、点到直线的距离公式,能求出结果方程.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$过点A(2,3),且F(2,0)为其右焦点,
∴椭圆C的左焦点为F′(-2,0),则|AF|=3,|AF′|=$\sqrt{(-2-2)^{2}+(0-3)^{2}}$=5,
∴$\left\{\begin{array}{l}{c=2}\\{2a=3+5}\end{array}\right.$,即$\left\{\begin{array}{l}{c=2}\\{a=4}\end{array}\right.$,∴b2=16-4=12,
∴椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.
(Ⅱ)设存在符合题意的直线l,其方程为y=$\frac{3}{2}x+t$,
由$\left\{\begin{array}{l}{y=\frac{3}{2}x+t}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$,整理,得3x2+3tx+t2-12=0,
∵直线l与椭圆C有公共点,
∴△=(3t)2-12(t2-12)=-3t2+144≥0,
解得-4$\sqrt{3}≤t≤4\sqrt{3}$,
∵直线OA与l的距离等于$\frac{10\sqrt{13}}{13}$,∴$\frac{|2t|}{\sqrt{9+4}}$=$\frac{10\sqrt{13}}{13}$,故t=±5.
∵±5∈[-4$\sqrt{3}$,4$\sqrt{3}$],
∴直线l的方程为y=$\frac{3}{2}x-5$或y=$\frac{3}{2}x+5$.
点评 本题考查椭圆方程和直线方程的求法,是中档题,解题时要认真审题,注意椭圆定义、根的判别式、点到直线的距离公式的合理运用.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
| A. | $\frac{4}{5}$ | B. | $\frac{5}{6}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
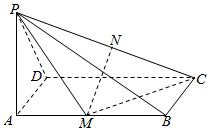 如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.
如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.