题目内容
19.已知$\left\{{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}}\right.$,若目标函数z=4ax+3by(a>0,b>0)最大值为12,则$\frac{1}{a}+\frac{1}{b}$的最小值为( )| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
分析 由已知利用线性规划可得a+b=1,而$\frac{1}{a}$+$\frac{1}{b}$=(a+b)($\frac{1}{a}$+$\frac{1}{b}$)展开后利用基本不等式即可求解
解答 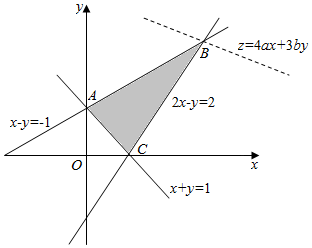 解:不等式表示的平面区域如图所示阴影部分,
解:不等式表示的平面区域如图所示阴影部分,
由直线4ax+3by=z(a>0,b>0)可得y=-$\frac{4a}{3b}$x+$\frac{z}{3b}$,
则$\frac{z}{3b}$表示直线在y轴截距,截距越大z越大,
由a>0,b>0可得-$\frac{4a}{3b}$<0,
∴直线4ax+3by=Z过点B时,目标函数有最大值,
由 $\left\{\begin{array}{l}{2x-y=2}\\{x-y=-1}\end{array}\right.$可得B(3,4),
此时目标函数z=4ax+3by(a>0,b>0)取得最大12,
即12a+12b=12,即a+b=1而$\frac{1}{a}$+$\frac{1}{b}$=($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=2+$\frac{b}{a}$+$\frac{a}{b}$≥4,
当且仅当$\frac{b}{a}$=$\frac{a}{b}$即a=b=$\frac{1}{2}$时取等号.
∴$\frac{1}{a}$+$\frac{1}{b}$的最小值4,
故选:C.
点评 本题综合地考查了线性规划问题和由基本不等式求函数的最值问题.要求能准确地画出不等式表示的平面区域,并且能够求得目标函数的最值.

练习册系列答案
相关题目
7.△ABC中,tanA,tanB是方程6x2-5x+1=0的两根,则tanC=( )
| A. | -1 | B. | 1 | C. | $-\frac{5}{7}$ | D. | $\frac{5}{7}$ |
14.对某产品1至6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如下表所示:
(Ⅰ)根据1至5月份的数据,求出y关于x的回归直线方程;
(Ⅱ)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
(Ⅲ)预计在今后的销售中,销售量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本).
参考公式:回归方程$\hat y=\hat bx+\hat a$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$.参考数据:$\sum_{i=1}^5{{x_i}{y_i}=392}$,$\sum_{i=1}^5{x_i^2}=502.5$.
| 月份i | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价xi(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi(件) | 11 | 10 | 8 | 6 | 5 | 14 |
(Ⅱ)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
(Ⅲ)预计在今后的销售中,销售量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本).
参考公式:回归方程$\hat y=\hat bx+\hat a$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$.参考数据:$\sum_{i=1}^5{{x_i}{y_i}=392}$,$\sum_{i=1}^5{x_i^2}=502.5$.
4.已知集合A={x|y=lgx},B={x|x2-2x-3<0},则A∩B=( )
| A. | (-1,0) | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-1,3) |
9.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一周期内的图象时,列表并填入了部分数据,如表:
(Ⅰ)根据如表求出函数f(x)的解析式;
(Ⅱ)设△ABC的三内角A,B,C的对边分别为a,b,c,且f(A)=$\sqrt{3}$,a=3,S为△ABC的面积,求S+3$\sqrt{3}$cosBcosC的最大值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | x1 | $\frac{π}{3}$ | x2 | $\frac{7π}{3}$ | x3 |
| y | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
(Ⅱ)设△ABC的三内角A,B,C的对边分别为a,b,c,且f(A)=$\sqrt{3}$,a=3,S为△ABC的面积,求S+3$\sqrt{3}$cosBcosC的最大值.