题目内容
8.已知圆C的方程为(x-1)2+y2=1,P是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上一点,过点P作图C的两条切线,切点为A,B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值是2$\sqrt{2}$-3.分析 设∠APB=2θ,令|$\overrightarrow{PC}$|2=x,由向量数量积公式得到$\overrightarrow{PA}•\overrightarrow{PB}$=x+$\frac{2}{x}$-3,由此能求出$\overrightarrow{PA}•\overrightarrow{PB}$的最小值.
解答 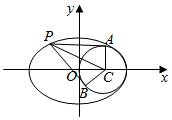 解:如图所示,设∠APB=2θ,
解:如图所示,设∠APB=2θ,
$\overrightarrow{PA}•\overrightarrow{PB}$=|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|cos2θ
=|$\overrightarrow{PA}$|2(2cos2θ-1)
=|$\overrightarrow{PA}$|2(2$\frac{|\overrightarrow{PA}{|}^{2}}{|\overrightarrow{PC}{|}^{2}}$-1),
令|$\overrightarrow{PC}$|2=x,得$\overrightarrow{PA}•\overrightarrow{PB}$=x+$\frac{2}{x}$-3,
∵x∈(1,9],∴$\overrightarrow{PA}•\overrightarrow{PB}$≥2$\sqrt{2}$-3,
当且仅当x=$\sqrt{2}$时,取等号,
故$\overrightarrow{PA}•\overrightarrow{PB}$的最小值是2$\sqrt{2}$-3.
点评 本题考查向量的数量积的最小值的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
12.对于集合{θ1,θ2,…,θ3}(n∈N*,n>2)及常数θ0,称$\frac{2}{n}[co{s}^{2}({θ}_{1}-{θ}_{0})+co{s}^{2}({θ}_{2}-{θ}_{0})+…+co{s}^{2}({θ}_{n}-{θ}_{0})]$为集合{θ1,θ2,…,θ3}相对于常数θ0的“余弦方差”,那么集合{$\frac{π}{3}$,$\frac{2π}{3}$,π}相对于常数α的“余弦方差”的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
19.已知$\left\{{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}}\right.$,若目标函数z=4ax+3by(a>0,b>0)最大值为12,则$\frac{1}{a}+\frac{1}{b}$的最小值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
13.下列函数中,不是偶函数的是( )
| A. | y=1-x2 | B. | y=tanx | C. | y=cos2x | D. | y=3x+3-x |
20.一个长方体底面为正方形且边长为4,高为h,若这个长方体能装下8个半径为1的小球和一个半径为2的大球,则h的最小值为( )
| A. | 8 | B. | 2+2$\sqrt{7}$ | C. | 2+2$\sqrt{5}$ | D. | 6 |
17.实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≤0\\ x+3y-3≥0\end{array}\right.$,则z=|x+y+1|的最大值为( )
| A. | 4 | B. | $2\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | 2 |
18.已知椭圆的焦点是F1、F2,P是椭圆的一个动点,如果M是线段F1P的中点,则动点M的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线的一支 | D. | 抛物线 |