题目内容
17.用红、黄、蓝三种颜色去涂图中标号为1,2…9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂颜色都不相同,且标号为“3,5,7”的小正方形涂相同的颜色,则符合条件的所有涂法共有( )种| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| A. | 18 | B. | 36 | C. | 72 | D. | 108 |
分析 分析图形中的3,5,7,有3种可能,当3,5,7,为其中一种颜色时,共6种可能,即可得出结论
解答 解:首先看图形中的3,5,7,有3种可能,
当3,5,7,为其中一种颜色时,2,6共有4种可能,其中2种2,6是涂相同颜色,各有2种可能,共6种可能.
4,8及9,与2,6及1,一样有6种可能并且与2,6,1,颜色无关.
当3,5,7换其他的颜色时也是相同的情况
符合条件的所有涂法共有3×6×6=108种,
故选:D.
点评 本题是一个排列组合的应用,考查分别计数原理,考查分类原理,是一个限制元素比较多的题目,解题时注意分类,做到不重不漏,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
7.命题“?n∈N*,$\frac{1}{n}$>$\frac{1}{n+1}$”的否定为( )
| A. | ?n∈N*,$\frac{1}{n}$≤$\frac{1}{n+1}$ | B. | ?n∈N*,$\frac{1}{n}$<$\frac{1}{n+1}$ | ||
| C. | ?n∈N*,$\frac{1}{{n}_{0}}$≤$\frac{1}{{n}_{0}+1}$ | D. | ?n0∈N*,$\frac{1}{{n}_{0}}$<$\frac{1}{{n}_{0}+1}$ |
8.已知不重合的直线m、l和平面α、β,m⊥α,l?β,则α∥β是“m⊥l”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
5.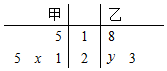 甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )
甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )
 甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )
甲乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲乙两人的平均数与中位数分别相等,则x:y为( )| A. | 3:2 | B. | 2:3 | C. | 3:1或5:3 | D. | 3:2或7:5 |
12.某校高二(1)班一次阶段考试数学成绩的茎叶图和频率分布直方图可见部分如图,根据图中的信息,可确定被抽测的人数及分数在[90,100]内的人数分别为( )


| A. | 20,2 | B. | 24,4 | C. | 25,2 | D. | 25,4 |
2.北京时间3月4日,CBA半决赛第四场,辽宁男篮客场战胜广东,总比分3:1淘汰对手紧急总决赛,辽宁与四川会师决赛,总决赛3月11日开打,采用7局4胜制(若某队取胜四场,则终止比赛,并获得本赛季冠军)采用2-3-2的赛程,由于辽宁常规赛占优,决赛时拥有主场优势(辽宁先两个主场,然后三个客场,再两个主场)以下是总决赛赛程:
(1)若考虑主场优势,每个队主场获胜的概率均为$\frac{2}{3}$,客场取胜的概率均为$\frac{1}{3}$,求辽宁队以比分4:1获胜的概率;
(2)若不考虑主场优势,每个队每场比赛获胜的概率均为$\frac{1}{2}$设本次决赛的比赛场数为X,求X的分布列及数学期望.
| 日期 | 比赛队 | 主场 | 客场 | 比赛时间 | 比赛地点 |
| 3月11日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
| 3月13日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
| 3月16日 | 四川-辽宁 | 四川 | 辽宁 | 19:35 | 成都 |
| 3月18日 | 四川-辽宁 | 四川 | 辽宁 | 19:35 | 成都 |
| 3月20日 | 四川-辽宁 | 四川 | 辽宁 | 19:35 | 成都 |
| 3月23日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
| 3月25日 | 辽宁-四川 | 辽宁 | 四川 | 19:35 | 本溪 |
(2)若不考虑主场优势,每个队每场比赛获胜的概率均为$\frac{1}{2}$设本次决赛的比赛场数为X,求X的分布列及数学期望.

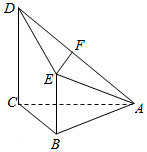 如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.
如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.