题目内容
8.已知不重合的直线m、l和平面α、β,m⊥α,l?β,则α∥β是“m⊥l”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
分析 m⊥α,l?β,α∥β,利用面面垂直的性质、线面垂直的性质可得:m⊥β,m⊥l.反之不成立,α与β可能相交.
解答 解:m⊥α,l?β,则α∥β⇒m⊥β,∴m⊥l.
反之不成立,α与β可能相交.
∴α∥β是“m⊥l”的充分不必要条件.
故选:A.
点评 本题考查了空间位置关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知函数f(x)=ax3+2bx2+3cx+4d(a,b,c,d为实数,a<0,c>0)是奇函数,且当x∈[0,1]时,f(x)的值域为[0,1],则c的最大值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
3.已知数列{bn}是等比数列,b9是1和3的等差中项,则b2b16=( )
| A. | 16 | B. | 8 | C. | 2 | D. | 4 |
13.若函数f(x)=asinx+2x+3,且f(-1)=7,则f(1)=( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
20.从高三的期末考试成绩中,选择了五位同学A,B,C,D,E,他们的考试成绩如表:
(1)从该小组语文低于130分的同学中任选2人,求选到的2人分数都在124以下的概率;
(2)从该小组同学中任选2人,求选到的2人的语文分数都在120以上且数学分都在[100,140)中的概率.
| A | B | C | D | E | |
| 语文 | 119 | 121 | 123 | 125 | 134 |
| 数学 | 123 | 141 | 118 | 122 | 132 |
(2)从该小组同学中任选2人,求选到的2人的语文分数都在120以上且数学分都在[100,140)中的概率.
17.用红、黄、蓝三种颜色去涂图中标号为1,2…9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂颜色都不相同,且标号为“3,5,7”的小正方形涂相同的颜色,则符合条件的所有涂法共有( )种
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| A. | 18 | B. | 36 | C. | 72 | D. | 108 |
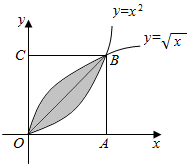 如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为$\frac{1}{3}$.
如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为$\frac{1}{3}$.
 如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.
如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.