题目内容
12.已知p:m∈(-2,-1),q:m满足$\frac{{x}^{2}}{2+m}-\frac{{y}^{2}}{m+1}=1$表示椭圆,那么p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 根据充分条件和必要条件的定义结合椭圆的方程进行判断即可.
解答 解:若足$\frac{{x}^{2}}{2+m}-\frac{{y}^{2}}{m+1}=1$表示椭圆,
则等价为$\frac{{x}^{2}}{m+2}$+$\frac{{y}^{2}}{-m-1}$=1,
则$\left\{\begin{array}{l}{m+2>0}\\{-m-1>0}\\{m+2≠-m-1}\end{array}\right.$即$\left\{\begin{array}{l}{m>-2}\\{m<-1}\\{m≠-\frac{3}{2}}\end{array}\right.$,
即-2<m<-1且m≠-$\frac{3}{2}$,
则p是q的必要不充分条件,
故选:B
点评 本题主要考查充分条件和必要条件的判断,根据椭圆的方程求出m的等价条件是解决本题的关键.

练习册系列答案
相关题目
20.若3a2-5b<0,则方程x5+2ax3+2bx+4c=0( )
| A. | 无实根 | B. | 有唯一实根 | C. | 有三个不同实根 | D. | 有五个不同实根 |
4.与如图所示的图象相符的函数是( )
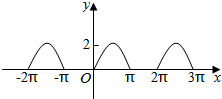

| A. | y=sinx-|sinx| | B. | y=|sinx|+sinx | C. | y=|sinx| | D. | y=|sinx|-sinx |
1.函数y=5sin2x+12cos2x的最小值和周期分别是( )
| A. | 5,π | B. | ,12,π | C. | ,-13,π | D. | -13,2π |