题目内容
10.已知实数x,y满足4x2+y2+3xy=1,则2x+y的最大值为$\frac{{2\sqrt{14}}}{7}$.分析 由题意和基本不等式整体变形可得2x+y的不等式,解不等式可得.
解答 解:∵实数x,y满足4x2+y2+3xy=1,
∴4x2+y2+4xy=1+xy,
∴(2x+y)2=1+$\frac{1}{2}$•2x•y≤1+$\frac{1}{2}$($\frac{2x+y}{2}$)2,
解关于2x+y的不等式可得2x+y≤$\frac{{2\sqrt{14}}}{7}$,
故答案为:$\frac{{2\sqrt{14}}}{7}$.
点评 本题考查基本不等式以及一元二次不等式的解集,属基础题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
20.过点(0,2b)的直线l与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的一条斜率为正值的渐近线平行,若双曲线C的右支上的点到直线l的距离恒大于b,则双曲线C的离心率的取值范围是( )
| A. | (1,2] | B. | (2,+∞) | C. | (1,2) | D. | (1,$\sqrt{2}$] |
5.已知全集U=R,集合A={x|($\frac{1}{2}$)x≤1,B={x|x2-6x+8≤0},则A∩B为( )
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
15.若非零向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow a+\overrightarrow b}|$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
20.若3a2-5b<0,则方程x5+2ax3+2bx+4c=0( )
| A. | 无实根 | B. | 有唯一实根 | C. | 有三个不同实根 | D. | 有五个不同实根 |
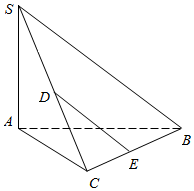 如图,在三棱锥S-ABC中,SA⊥底面ABC,BC⊥AC,D、E分别是SC、BC的中点.
如图,在三棱锥S-ABC中,SA⊥底面ABC,BC⊥AC,D、E分别是SC、BC的中点.