题目内容
3.已知函数$f(x)=2\sqrt{2}cosxsin(x+\frac{π}{4})$.(Ⅰ)求函数f(x)的最小正周期及图象的对称轴方程;
(Ⅱ)求函数f(x)的单调区间.
分析 (Ⅰ)由条件利用三角恒等变换,正弦函数的周期性、以及图象的对称性,得出结论.
(Ⅱ)由条件利用正弦函数的单调性,求得函数f(x)的单调区间.
解答 解:(Ⅰ)对于函数$f(x)=2\sqrt{2}cosxsin(x+\frac{π}{4})$=2$\sqrt{2}$cosx•(sinx•$\frac{\sqrt{2}}{2}$+cosx•$\frac{\sqrt{2}}{2}$)
=sin2x+2•cos2x=sin2x+cos2x+1=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,它的最小正周期为$\frac{2π}{2}$=π,
令2x+$\frac{π}{4}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{π}{8}$,可得函数的图象的对称轴方程为x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z.
(Ⅱ)令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,
可得函数f(x)的单调增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
2kπ+$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,
可得函数f(x)的单调减区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
点评 本题主要考查三角恒等变换,正弦函数的周期性、单调性以及图象的对称性,属于中档题.

| A. | 若“p∨q”为假命题,则p,q均为假命题 | |
| B. | “x=1”是“x≥1”的充分不必要条件 | |
| C. | 若命题p:?x0∈R,x${\;}_{0}^{2}$≥0,则命题¬p:?x∈R,x2<0 | |
| D. | “sinx=$\frac{1}{2}$”的必要不充分条件是“x=$\frac{π}{6}$” |
| A. | (-2,-1]∪[3,+∞) | B. | $(-\frac{5}{3},-1)∪(3,+∞)$ | C. | $[-\frac{5}{3},-1]∪[3,+∞)$ | D. | (-2,-1)∪(3,+∞) |
| A. | -1-2i | B. | 1-2i | C. | -1+2i | D. | 1+2i |
| A. | 103 | B. | 102 | C. | 100 | D. | 98 |
| A. | 8-5$\sqrt{3}$ | B. | 6-5$\sqrt{3}$ | C. | 5$\sqrt{3}$-8 | D. | 5$\sqrt{3}$-6 |
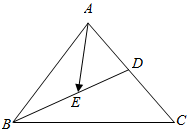 如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.