题目内容
9．已知圆x2+y2+2mx+2y=0的半径是1，则圆心坐标为（ ）| A． | （0，-1） | B． | （1，-1） | C． | （-1，0） | D． | （-1，1） |
分析 利用配方法化圆的一般方程为标准方程，从而求得圆的圆心坐标和半径．
解答 解：由x2+y2+2mx+2y=0，配方得（x+m）2+（y+1）2=m2+1．
∴圆的圆心坐标为C（-m，-1），半径为$\sqrt{{m}^{2}+1}$=1，
∴m=0，圆心坐标为C（0，-1），
故选A．
点评 本题考查圆的一般方程化标准方程，考查配方法，是基础题．
练习册系列答案
相关题目
19．抛物线y2=2px（p＞0）的焦点为F，准线为l，A，B是抛物线上的两个动点，且满足∠AFB=$\frac{π}{2}$．设线段AB的中点M在l上的投影为N，则$\frac{{|{AB}|}}{{|{MN}|}}$的最小值是（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |
4．下列说法中正确的是（ ）
| A． | 任一事件的概率总在（0，1）内 | B． | 不可能事件的概率不一定为0 | ||
| C． | 必然事件的概率一定为1 | D． | 概率为0的事件一定是不可能事件 |
14．不等式2x2-x-1＞0的解集是（ ）
| A． | $\{x|-\frac{1}{2}＜x＜1\}$ | B． | {x|x＞1} | C． | {x|x＜1或x＞2} | D． | $\{x|x＜-\frac{1}{2}或x＞1\}$ |
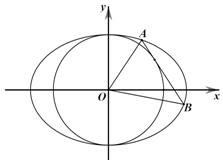如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1（a＞b＞0）过点（0，1）和（1，$\frac{\sqrt{2}}{2}$），圆O：x2+y2=b2