题目内容
10．
如图，三棱锥P-ABC中，E，F分别是AB，BC的中点，M，N分别是PE，PF上的点．（1）M，N分别是PE，PF的中点时，求证：MN∥平面ABC．
（2）当MN∥平面ABC时，求证：MN∥AC．
分析 （1）连接EF，由M，N分别是PE，PF的中点，可得MN∥EF，结合线面平行的判断可得MN∥平面ABC．
（2）由E，F分别是AB，BC的中点，可得EF∥AC，由线面平行的性质得MN∥EF，再由平行公理可得MN∥AC．
解答 
证明：（1）如图，连接EF，
∵M，N分别是PE，PF的中点，
∴MN为△PEF的中位线，
∴MN∥EF，
又EF?平面ABC，MN?平面ABC，
∴MN∥平面ABC．
（2）∵E，F分别是AB，BC的中点，
∴EF为△ABC的中位线，
∴EF∥AC，
由MN∥平面ABC，MN?平面PEF，且平面PEF∩平面ABC=EF，
∴MN∥EF，
∴MN∥AC．
点评 本题考查直线与平面平行的判定和性质，考查了空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
20．若定义域为R的奇函数y=f（x）有反函数y=f-1（x），那么必在函数y=f-1（x+1）图象上的点是（ ）
| A． | （-f（t-1），-t） | B． | （-f（t+1），-t） | C． | （-f（t）-1，-t） | D． | （-f（t）+1，-t） |
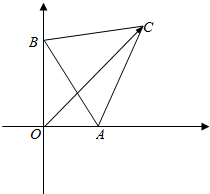如图，线段AB长度为2，点A，B分别在x轴的正半轴和y轴的正半轴上滑动，以线段AB为一边，在第一象限内作等边三角形，O为坐标原点，则$\overrightarrow{OC}$•$\overrightarrow{OB}$的取值范围是[0，3]．
19．角α 终边经过点（-sin20°，cos20°），则角α的最小正角是（ ）
| A． | 110°? | B． | 160°? | C． | 290°? | D． | 340°? |
20．设全集U={1，2，3，4，5}，集合A={1，2，4}，B={4，5}，则集合A∩（∁UB）=（ ）
| A． | {1，2} | B． | {3，5} | C． | {4} | D． | {5} |