题目内容
5.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0.则f(3),f(-1),f(2)的大小关系是f(3)<f(2)<f(-1).分析 由偶函数性质可得f(-1)=f(1),结合函数f(x)在[0,+∞)为减函数,可得结论.
解答 解:∵函数f(x)是定义在R上的偶函数,
∴f(-1)=f(1),
又∵对任意的x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0.
∴函数f(x)在[0,+∞)为减函数,
∴f(3)<f(2)<f(1),
即f(3)<f(2)<f(-1),
故答案为:f(3)<f(2)<f(-1)
点评 本题考查的知识点是函数的单调性,函数的奇偶性,是函数图象和性质的简单综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,三棱锥P-ABC中,E,F分别是AB,BC的中点,M,N分别是PE,PF上的点.
如图,三棱锥P-ABC中,E,F分别是AB,BC的中点,M,N分别是PE,PF上的点.
(1)M,N分别是PE,PF的中点时,求证:MN∥平面ABC.
(2)当MN∥平面ABC时,求证:MN∥AC.
 如图,三棱锥P-ABC中,E,F分别是AB,BC的中点,M,N分别是PE,PF上的点.
如图,三棱锥P-ABC中,E,F分别是AB,BC的中点,M,N分别是PE,PF上的点.(1)M,N分别是PE,PF的中点时,求证:MN∥平面ABC.
(2)当MN∥平面ABC时,求证:MN∥AC.
15.若函数y=2sin(x+θ)的图象向右平移$\frac{π}{6}$个单位,再向上平移2个单位后,它的一条对称轴是$x=\frac{π}{4}$,则θ的一个可能的值是( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
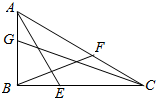 如图,△ABC中,点E、F、G分别在边BC、AC、AB上,且$\frac{AG}{GB}$=$\frac{BE}{EC}$=$\frac{CF}{FA}$=$\frac{1}{2}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,△ABC中,点E、F、G分别在边BC、AC、AB上,且$\frac{AG}{GB}$=$\frac{BE}{EC}$=$\frac{CF}{FA}$=$\frac{1}{2}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.