题目内容
1．直线xcosθ+ysinθ+a=0与xsinθ-ycosθ+b=0的位置关系是垂直．分析 由两直线中x，y的系数积之和为0，得到这两条直线垂直．
解答 解：∵直线xcosθ+ysinθ+a=0与xsinθ-ycosθ+b=0，
∴x，y的系数积之和：cosθsinθ+sinθ（-cosθ）=0，
∴这两条直线垂直．
故答案为：垂直．
点评 本题考查两直线的位置关系的判断，是基础题，解题时要认真审题，注意两直线平行与垂直的性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
11．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | 4π | B． | $\frac{20π}{3}$ | C． | 12π | D． | 5π |
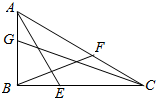如图，△ABC中，点E、F、G分别在边BC、AC、AB上，且$\frac{AG}{GB}$=$\frac{BE}{EC}$=$\frac{CF}{FA}$=$\frac{1}{2}$，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$．
如图，三棱锥P-ABC中，E，F分别是AB，BC的中点，M，N分别是PE，PF上的点．